题目内容
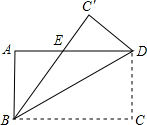
 如图,把长方形ABCD沿AC折叠,AD落在AD′处,AD′交BC于点E,已知AB=2cm,BC=4cm.(长方形的对边相等,四个角都为直角)
如图,把长方形ABCD沿AC折叠,AD落在AD′处,AD′交BC于点E,已知AB=2cm,BC=4cm.(长方形的对边相等,四个角都为直角)
(1)求证:AE=EC;
(2)求EC的长;
(3)求重叠部分的面积.
解:(1)∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠B=90°,AD∥BC,
∴∠DAC=∠BCA.
∵△ADC与△AD′C关于AC成轴对称
∴△ADC≌△AD′C,
∴∠DAC=∠D′AC,
∴∠D′AC=∠ACB,
∴AE=EC;
(2)∵AB=2cm,BC=4cm,
∴CD=2cm,AD=4cm.
设EC=x,就有AE=x,BE=4-x,在Rt△ABE中,由勾股定理,得
4+(4-x)2=x2,
解得:x=2.5.
答:EC的长为2.5cm;
(3)∵S△AEC= ,
,
S△AEC= =2.5cm2.
=2.5cm2.
答:重叠部分的面积为2.5cm2.
分析:(1)根据轴对称的性质和矩形的性质就可以得出∠EAC=∠ECA,就可以得出AE=CE,
(2)设EC=x,就有AE=x,BE=4-x,在Rt△ABE中,由勾股定理就可以求出结论;
(3)根据(2)的结论直接根据三角形的面积公式就可以求出结论.
点评:本题考查了矩形的性质的运用,勾股定理的运用,轴对称的性质的运用,平行线的性质的运用,解答时运用勾股定理求出EC的值是关键.
∴AB=CD,AD=BC,∠B=90°,AD∥BC,

∴∠DAC=∠BCA.
∵△ADC与△AD′C关于AC成轴对称
∴△ADC≌△AD′C,
∴∠DAC=∠D′AC,
∴∠D′AC=∠ACB,
∴AE=EC;
(2)∵AB=2cm,BC=4cm,
∴CD=2cm,AD=4cm.
设EC=x,就有AE=x,BE=4-x,在Rt△ABE中,由勾股定理,得
4+(4-x)2=x2,
解得:x=2.5.
答:EC的长为2.5cm;
(3)∵S△AEC=
 ,
,S△AEC=
 =2.5cm2.
=2.5cm2.答:重叠部分的面积为2.5cm2.
分析:(1)根据轴对称的性质和矩形的性质就可以得出∠EAC=∠ECA,就可以得出AE=CE,
(2)设EC=x,就有AE=x,BE=4-x,在Rt△ABE中,由勾股定理就可以求出结论;
(3)根据(2)的结论直接根据三角形的面积公式就可以求出结论.
点评:本题考查了矩形的性质的运用,勾股定理的运用,轴对称的性质的运用,平行线的性质的运用,解答时运用勾股定理求出EC的值是关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目

 如图,把长方形ABCD(AB=CD,AD=BC,∠A=∠ABC=∠C=∠CDA=90°)沿对角线BD对折,使点C落在点C,处,请说明AE=C′E.
如图,把长方形ABCD(AB=CD,AD=BC,∠A=∠ABC=∠C=∠CDA=90°)沿对角线BD对折,使点C落在点C,处,请说明AE=C′E.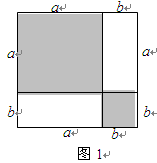
 ,
, .
. .
. >0.
>0.

 如图,把长方形ABCD(AB=CD,AD=BC,∠A=∠ABC=∠C=∠CDA=90°)沿对角线BD对折,使点C落在点C,处,请说明AE=C′E.
如图,把长方形ABCD(AB=CD,AD=BC,∠A=∠ABC=∠C=∠CDA=90°)沿对角线BD对折,使点C落在点C,处,请说明AE=C′E.