题目内容
【题目】我们约定,在平面直角坐标系![]() 中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点
中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点![]() 的参照线有:
的参照线有:![]() ,
,![]() ,
,![]() ,
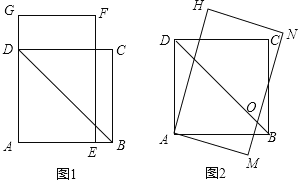
,![]() (如图1).
(如图1).
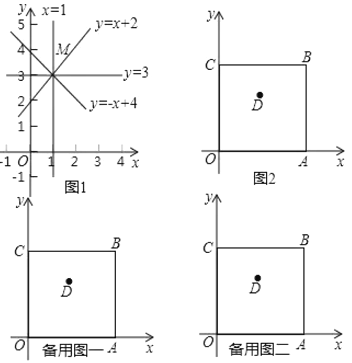
如图2,正方形![]() 在平面直角坐标系
在平面直角坐标系![]() 中,点
中,点![]() 在第一象限,点
在第一象限,点![]() ,
,![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 在正方形内部.
在正方形内部.
(1)直接写出点![]() 的所有参照线: ;
的所有参照线: ;
(2)若![]() ,点
,点![]() 在线段
在线段![]() 的垂直平分线上,且点
的垂直平分线上,且点![]() 有一条参照线是
有一条参照线是![]() ,则点
,则点![]() 的坐标是_______________;
的坐标是_______________;
(3)在(2)的条件下,点![]() 是
是![]() 边上任意一点(点
边上任意一点(点![]() 不与点
不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,将
,将![]() 沿着
沿着![]() 折叠,点
折叠,点![]() 的对应点记为
的对应点记为![]() .当点
.当点![]() 在点
在点![]() 的平行于坐标轴的参照线上时,写出相应的折痕
的平行于坐标轴的参照线上时,写出相应的折痕![]() 所在直线的解析式: .
所在直线的解析式: .
【答案】(1)x=m,y=n,y=x+n-m,y=-x+n+m;(2)(3,4);(3)![]() 或
或![]() .
.
【解析】
(1)根据参照线的定义可知,点D(m,n)的所有参照线为:x=m,y=n,y=x+n-m,y=-x+n+m;
(2)利用待定系数法即可解决问题;
(3)分两种情形①如图1中,当点A′在参照线HM上时,设PA=PA′=x.②如图2中,当点A′在参照线DH上时,设PA=PA′=y.分别构建方程即可解决问题;
解:(1)根据参照线的定义可知,点D(m,n)的所有参照线为:x=m,y=n,y=x+n-m,y=-x+n+m,
故答案为x=m,y=n,y=x+n-m,y=-x+n+m
(2)∵A(6,0),点D在线段OA的垂直平分线上,
∴点D的横坐标为3,
又∵点D有一条参照线是y=-x+7,
∴x=3时,y=-3+7=4,
∴点D坐标为(3,4),
故答案为(3,4).
(3)①如图1中,当点A′在参照线HM上时,设PA=PA′=x.

易知 ![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
∴直线OP的解析式为:
![]()
②如图2中,当点A′在参照线DH上时,设PA=PA′=y.
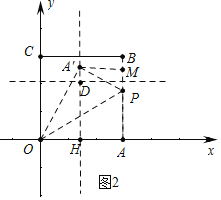
易知 ![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
∴直线OP的解析式为:
![]()
故答案为: ![]() 或
或![]() .
.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应数值:
的几组对应数值:
| … |
|
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| 0 |
|
|
|
| 2 |
|
| … |
①写出![]() 的值为 ;
的值为 ;
②在平面直角坐标系中,描出了以表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
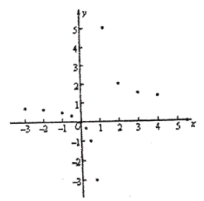
(3)当![]() 时,直接写出x的取值范围为: .
时,直接写出x的取值范围为: .