题目内容
如图,⊙O1和⊙O2相交于A、B两点,且AO1、AO2分别是⊙O2、⊙O1的切线,A是切点,若⊙O1的半径r=3,⊙O2的半径R=4,求公共弦AB的长.
【答案】分析:连接O1O2交AB于点C,由题意可知,O1A⊥O2A,故可由三角形O1AO2面积公式来求解AC的长,从而求得AB的长.
解答: 解:连接O1O2交AB于点C,如下图所示:
解:连接O1O2交AB于点C,如下图所示:
∵AO1、AO2分别是⊙O2、⊙O1的切线,
∴O1A⊥O2A,
∵AB为两圆的公共弦,O1O2为两圆的圆心距,
∴O1O2⊥AB且平分AB;
∵S△O1AO2= ×O1A×O2A=
×O1A×O2A= O1O2×AC,
O1O2×AC,
∴AC=O1A×O2A÷O1O2= ,
,
∴AB= .
.
答:公共弦AB的长为 .
.
点评:本题主要考查了相交圆的性质及直角三角形面积公式的不同表达形式.
解答:
 解:连接O1O2交AB于点C,如下图所示:
解:连接O1O2交AB于点C,如下图所示:∵AO1、AO2分别是⊙O2、⊙O1的切线,
∴O1A⊥O2A,
∵AB为两圆的公共弦,O1O2为两圆的圆心距,
∴O1O2⊥AB且平分AB;
∵S△O1AO2=
 ×O1A×O2A=
×O1A×O2A= O1O2×AC,
O1O2×AC,∴AC=O1A×O2A÷O1O2=
 ,
,∴AB=
 .
.答:公共弦AB的长为
 .
.点评:本题主要考查了相交圆的性质及直角三角形面积公式的不同表达形式.

练习册系列答案
相关题目
 20、已知:如图,⊙O1和⊙O2相交于A、B两点,动点P在⊙O2上,且在⊙1外,直线PA、PB分别交⊙O1于C、D,问:⊙O1的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明.
20、已知:如图,⊙O1和⊙O2相交于A、B两点,动点P在⊙O2上,且在⊙1外,直线PA、PB分别交⊙O1于C、D,问:⊙O1的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明.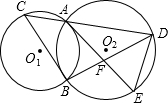 长⊙O1相交于C点,连接BC,过A点作AE∥BC与⊙O相交于E点,与BD相交于F点.
长⊙O1相交于C点,连接BC,过A点作AE∥BC与⊙O相交于E点,与BD相交于F点.
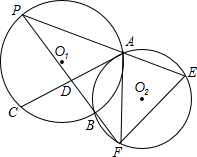 、PB的延长线分别交⊙O2于点E、F,PB交AC于D.
、PB的延长线分别交⊙O2于点E、F,PB交AC于D. 16、如图.⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点,求证:AB⊥AC.
16、如图.⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点,求证:AB⊥AC. (2001•黄冈)已知,如图,⊙O1和⊙O2内切于点P,过点P的直线交⊙O1于点D,交⊙O2于点E;DA与⊙O2相切,切点为C.
(2001•黄冈)已知,如图,⊙O1和⊙O2内切于点P,过点P的直线交⊙O1于点D,交⊙O2于点E;DA与⊙O2相切,切点为C.