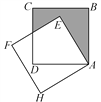
题目内容
【题目】如图,将边为![]() 的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
A. ![]() -
-![]() B. 3-
B. 3-![]() C. 2-
C. 2-![]() D. 2-
D. 2-![]()
【答案】B
【解析】分析:连接AG,根据∠BAE=30°可知∠DAE=60°,由正方形的性质可知,AB=AD,由图形旋转的性质可知AD=AE,故可得出Rt△ADG≌Rt△AEG,由直角三角形的性质可得出DG的长,再由S 阴影=![]() ,即可得出结论.
,即可得出结论.
本题解析:

连接AG,
∵∠BAE=30°,
∴∠DAE=60°,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠B=90°,
∵正方形AEFH是正方形ABCD旋转而成,
∴AD=AE,∠E=90°,
在Rt△ADG与Rt△AEG中,AD=AE,AG=AG,
∴Rt△ADG≌Rt△AEG,
∴∠DAG= ∠EAG =30°,
∴DG=ADtan∠DAG=![]() ×
×![]() =1,
=1,
∴![]()
∴S 四边形ADGE=2![]() =2×
=2×![]() =
=![]() ,
,
∴S 阴影=![]() ,故选B.
,故选B.

练习册系列答案
相关题目