题目内容
【题目】如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8cm,BC=4cm,AB=5cm.从初始时刻开始,动点P,Q 分别从点A,B同时出发,运动速度均为1cm/s,动点P沿A﹣B﹣﹣C﹣﹣E的方向运动,到点E停止;动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动,到点D停止,设运动时间为xs,△PAQ的面积为ycm2,(这里规定:线段是面积为0的三角形)
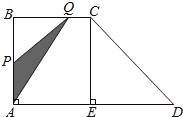
解答下列问题:
(1)当x=2s时,y= cm2;当x=![]() s时,y= cm2.
s时,y= cm2.
(2)当5≤x≤14 时,求y与x之间的函数关系式.
(3)当动点P在线段BC上运动时,求出![]() 时x的值.
时x的值.
(4)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值.
【答案】(1)2;9(2)(2)当5≤x≤9时,y=![]() x2-7x+
x2-7x+![]() ;当9<x≤13时, y=-
;当9<x≤13时, y=-![]() x2+
x2+![]() x-35;当13<x≤14时,y=-4x+56;(3)y=
x-35;当13<x≤14时,y=-4x+56;(3)y=![]() (4)
(4)![]() 、
、![]() 或
或![]()
【解析】
试题分析:(1)当x=2s时,AP=2,BQ=2,利用三角形的面积公式直接可以求出y的值,当x=![]() s时,三角形PAQ的高就是4,底为4.5,由三角形的面积公式可以求出其解.
s时,三角形PAQ的高就是4,底为4.5,由三角形的面积公式可以求出其解.
(2)当5≤x≤14 时,求y与x之间的函数关系式.要分为三种不同的情况进行表示:当5≤x≤9时,当9<x≤13时,当13<x≤14时.
(3)可以由已知条件求出![]() ,然后根据条件求出y值,代入当5≤x≤9时的解析式就可以求出x的值.
,然后根据条件求出y值,代入当5≤x≤9时的解析式就可以求出x的值.
(4)利用相似三角形的性质,相似三角形的对应线段成比例就可以求出对应的x的值.
试题解析:(1)当x=2s时,AP=2,BQ=2,
∴y=![]() =2
=2
当x=![]() s时,AP=4.5,Q点在EC上
s时,AP=4.5,Q点在EC上
∴y=![]() =9
=9
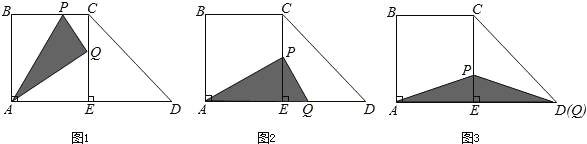
(2)当5≤x≤9时(如图1)
y=![]() =
=![]() (5+x-4)×4-
(5+x-4)×4-![]() ×5(x-5)-
×5(x-5)-![]() (9-x)(x-4)
(9-x)(x-4)
y=![]() x2-7x+
x2-7x+![]()
当9<x≤13时(如图2)
y=![]() (x-9+4)(14-x)
(x-9+4)(14-x)
y=-![]() x2+
x2+![]() x-35
x-35
当13<x≤14时(如图3)
y=![]() ×8(14-x)
×8(14-x)
y=-4x+56;
(3)当动点P在线段BC上运动时,
∵y=![]() =
=![]() ×
×![]() (4+8)×5=8
(4+8)×5=8
∴8=![]() x2-7x+
x2-7x+![]() ,即x2-14x+49=0,解得:x1=x2=7
,即x2-14x+49=0,解得:x1=x2=7
∴当x=7时,y=![]()
(4)设运动时间为x秒,
当PQ∥AC时,BP=5-x,BQ=x,
此时△BPQ∽△BAC,
故![]() ,即
,即![]() ,
,
解得x=![]() ;
;
当PQ∥BE时,PC=9-x,QC=x-4,
此时△PCQ∽△BCE,
故![]() ,即
,即![]() ,
,
解得x=![]() ;
;
当PQ∥BE时,EP=14-x,EQ=x-9,
此时△PEQ∽△BAE,
故![]() ,即
,即![]() ,
,
解得x=![]() .
.
综上所述x的值为:x=![]() 、
、![]() 或
或![]() .
.

【题目】在我市实施“城乡环境综合治理”期间,某校组织学生开展“走出校门,服务社会”的公益活动.八年级一班王浩根据本班同学参加这次活动的情况,制作了如下的统计图表:
该班学生参加各项服务的频数、频率统计表:
服务类别 | 频数 | 频率 |
文明宣传员 | 4 | 0.08 |
文明劝导员 | 10 | |
义务小警卫 | 8 | 0.16 |
环境小卫士 | 0.32 | |
小小活雷锋 | 12 | 0.24 |
请根据上面的统计图表,解答下列问题:

(1)该班参加这次公益活动的学生共有 名;
(2)请补全频数、频率统计表和频数分布直方图;
(3)若八年级共有900名学生报名参加了这次公益活动,试估计参加文明劝导的学生人数.

