Question

【题目】如图，已知将沿所在直线翻折，点恰好与上的点重合，对折边，折痕也经过点，则下列说法正确的是（ ）

①；

②；

③；

④；

⑤若，则是等边三角形．

A. 只有①②正确 B. ①②③

C. ①②③④ D. ①②③④⑤

Answer 1

【答案】D

【解析】

①正确，根据B、C关于AD对称即可证明．

②正确，先证明AB=AC，再证明CA=CE即可．

③正确，根据AB=CE，BD=CD，即可证明．

④正确，根据三角形面积公式即可证明．

⑤正确，只要证明∠ACB=60°即可．

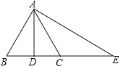
∵B、C关于直线AD对称，

∴AD⊥BC，BD=DC，

∴AB=AC，∠ADC=90°，故①正确，

∵对折边AE，折痕也经过点C，

∴CA=CE，

∴AB=AC=CE，故②正确，

∵AB+BD=CE+CD=DE，故③正确，

S△ACD：S△ACE=CDAD：CEAD=CD：CE，故④正确，

∵CA=CE，∠E=30°，

∴∠CAE=∠E=30°，

∴∠ACE=∠E+∠CAE=60°，

∵AB=AC，

∴△ABC是等边三角形．故⑤正确．

∴①②③④⑤正确，

故选D．