题目内容
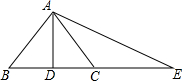如图所示，AD垂直平分BC，点C在AE的垂直平分线上，AB+BD与DE的关系是________．
AB+BD=DE
分析：根据AD垂直平分BC可知AB=AC，BD=CD，由于C在AB的垂直平分线上，故AB=AC=CE，即AB+BD=DE．
解答：∵AD垂直平分BC，
∴AB=AC，BD=CD，
∵C在AE的垂直平分线上，
∴AB=AC=CE，
∴AB+BD=DE．
故答案为：AB+BD=DE．
点评：本题考查的是线段垂直平分线的性质及等腰三角形的性质，熟知线段垂直平分线的性质是解答此题的关键．
分析：根据AD垂直平分BC可知AB=AC，BD=CD，由于C在AB的垂直平分线上，故AB=AC=CE，即AB+BD=DE．
解答：∵AD垂直平分BC，
∴AB=AC，BD=CD，
∵C在AE的垂直平分线上，
∴AB=AC=CE，
∴AB+BD=DE．
故答案为：AB+BD=DE．
点评：本题考查的是线段垂直平分线的性质及等腰三角形的性质，熟知线段垂直平分线的性质是解答此题的关键．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
