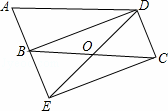
题目内容
如图,边长为1的正方形ABCD一边AD在x负半轴上,直线l:y= x+2经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线y=﹣x2+bx+c顶点E在直线l上.
x+2经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线y=﹣x2+bx+c顶点E在直线l上.
(1)求A,D两点的坐标及抛物线经过A,D两点时的解析式;
(2)当抛物线的顶点E(m,n)在直线l上运动时,连接EA,ED,试求△EAD的面积S与m之间的函数解析式,并写出m的取值范围;
(3)设抛物线与y轴交于G点,当抛物线顶点E在直线l上运动时,以A,C,E,G为顶点的四边形能否成为平行四边形?若能,求出E点坐标;若不能,请说明理由.
解:(1)∵直线l:y= x+2经过点B(x,1),
x+2经过点B(x,1),
∴1=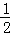 x+2,解得x=﹣2,
x+2,解得x=﹣2,
∴B(﹣2,1) ,
,
∴A(﹣2,0),D(﹣3,0),
∵抛物线经过A,D两点,
∴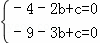 ,解得
,解得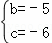 ,
,
∴抛物线经过A,D两点时的解析式为y═﹣x2﹣5x﹣6;
(2)∵顶点E(m,n)在直线l上,
∴n=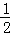 m+2,
m+2,
∴S=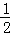 ×1×(
×1×(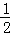 m+2)=
m+2)=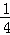 m+1,
m+1,
即S=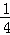 m+1(m≠4);
m+1(m≠4);
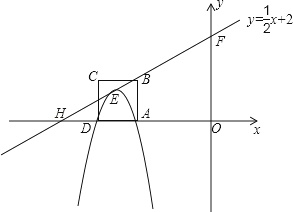
(3)如图,若以A,C,E,G为顶点的四边形能成为平行四边形,则AC=EQ,AC∥EQ,
作EH∥y轴交过Q点平行于x轴的直线相交于H,则EH⊥QH,△EHQ≌△CDA,
∴QH=AD=1,
∴E的横坐标为±1,
∵顶点E在直线l上,
∴y= ×(﹣1)+2=
×(﹣1)+2=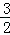 ,或y=
,或y= ×1+2=
×1+2=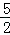
∴E(﹣1,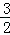 )或(1,
)或(1,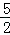 ).
).


练习册系列答案
相关题目
下列运算正确的是( )
|
| A. |
| B. | 3x2y﹣x2y=3 |
|
| C. |
| D. |
|
下列运算正确的是( )
|
| A. | (x﹣2)2=x2﹣4 | B. | x3•x4=x12 | C. | x6÷x3=x2 | D. | (x2)3=x6 |
 =____________________________.
=____________________________.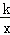 的图象交于A、B两点,其中点A的坐标为(2,3).
的图象交于A、B两点,其中点A的坐标为(2,3).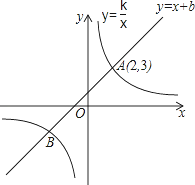
 的所有整数解的积为
的所有整数解的积为 
 +
+ =
=
 =a+b
=a+b (a2b)3=a6b3
(a2b)3=a6b3