题目内容
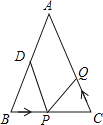
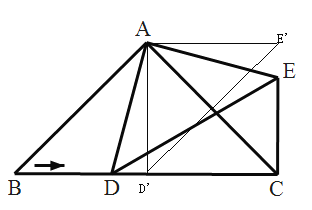
【题目】已知等腰![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发在线段
出发在线段![]() 移动,以
移动,以![]() 为腰作等腰
为腰作等腰![]() ,
,![]() ,连接
,连接![]() .
.
(1)如图,求证:![]() ≌
≌![]() ;
;
(2)求证:![]() ;
;
(3)若![]() ,试问:
,试问:![]() 的面积有没有最大值,如没有请说明理由,如有请求出最大值.
的面积有没有最大值,如没有请说明理由,如有请求出最大值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() 最小时,
最小时,![]() 最大,最大值为
最大,最大值为![]()
【解析】
(1)由△ABC和△ADE都是等腰Rt△可得,AB=AC,AD=AE,∠BAC=∠DAE=90°,则有∠BAD=∠CAE,从而可证到△ACE≌△ABD;
(2)由△ACE≌△ABD可得∠ACE=∠ABD=45°,从而得到∠BCE=∠BCA+∠ACE=90°;由勾股定理得![]() ,
,![]() ,从而可得结论;
,从而可得结论;
(3)由△ACE≌△ABD可得![]() ,当
,当![]() 最小时,
最小时,![]() 最大,从而可得结论.
最大,从而可得结论.
(1)∵![]() 和
和![]() 都是等腰
都是等腰![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
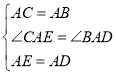 ,
,
∴![]() ≌
≌![]() ;
;
(2)∵△ACE≌△ABD,
∴∠ACE=∠ABD=45°,
∵![]() 是等腰三角形,
是等腰三角形,
∴∠ABD=45°,
∴∠BCE=∠BCA+∠ACE=90°,
∴![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
(3)∵△ACE≌△ABD,
∴![]() =
=![]() ,
,
而![]()
所以,当![]() 最小时,
最小时,![]() 最大,如图,当AD’⊥BC时,
最大,如图,当AD’⊥BC时,![]() 最小,
最小,
∵AB=4,∴AD’=ABcos45°=2![]()
∴![]() =
=![]() ×AD’2=4
×AD’2=4
∴![]() 最大为8-4=
最大为8-4=![]() .
.

练习册系列答案
相关题目