题目内容
已知关于x的方程x2+2x+m+1=0有两个相等的实数根，解方程x2+3mx+1-2m=0．
考点：根的判别式
专题：
分析：首先根据原方程根的情况，利用根的判别式求出m的值，将m的值代入x2+3mx+1-2m=0，即可求解．
解答：解：∵关于x的一元二次方程x2+2x+m+1=0有两个相等的实数根，
∴△=b2-4ac=22-4×1×（m+1）=-4m=0，
∴m=0，
∴方程x2+3mx+1-2m=0即为x2+1=0，
∵△=b2-4ac=02-4×1×1=-4＜0，
∴原方程无实数根．
∴△=b2-4ac=22-4×1×（m+1）=-4m=0，
∴m=0，
∴方程x2+3mx+1-2m=0即为x2+1=0，
∵△=b2-4ac=02-4×1×1=-4＜0，
∴原方程无实数根．
点评：此题考查了根的判别式，一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
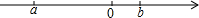实数a、b在数轴上的位置如图所示，给出如下结论：①a+b＞0；②b-a＞0；③-a＞b；④a＞-b，⑤|a|＞|b|＞0．其中正确的结论是（ ）| A、①②③ | B、②③④ |
| C、②③⑤ | D、②④⑤ |
下列命题：
①由不在同一直线上的三条线段首尾依次相接所组成的图形叫做三角形；
②在三角形中，连接一个顶点和对边中点的直线叫做三角形的中线；
③任何三角形都有三条中线、三条内角平分线，它们都相交于一点；
④直角三角形的高只有一条．
其中正确的命题有（ ）
①由不在同一直线上的三条线段首尾依次相接所组成的图形叫做三角形；
②在三角形中，连接一个顶点和对边中点的直线叫做三角形的中线；
③任何三角形都有三条中线、三条内角平分线，它们都相交于一点；
④直角三角形的高只有一条．
其中正确的命题有（ ）
| A、一个 | B、两个 | C、三个 | D、四个 |
买一斤土豆需要x元，买一斤白菜需要y元，则买6斤土豆、8斤白菜共需要（ ）
| A、（6x+8y）元 |
| B、48xy元 |
| C、（8x+6y）元 |
| D、14xy元 |
下列长度的三条线段能组成三角形的是（ ）
| A、6，8，10 |
| B、4，5，9 |
| C、1，2，4 |
| D、5，15，8 |