题目内容
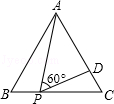
如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为( )

A.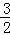 | B.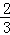 | C.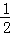 | D.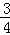 |
B
试题分析:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠APB=∠PAC+∠C,∠PDC=∠PAC+∠APD,
∵∠APD=60°,
∴∠APB=∠PAC+60°,∠PDC=∠PAC+60°,
∴∠APB=∠PDC,
又∵∠B=∠C=60°,
∴△ABP∽△PCD,
∴
 =
= ,即
,即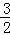 =
= ,
,∴CD=
 .
.故选B.
点评:本题考查了相似三角形的性质和判定.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
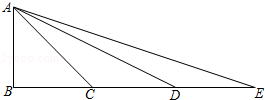
 、
、 分别在
分别在 的边
的边 、
、 上,要使△AED∽△ABC,应添加条件是 ;(只写出一种即可).
上,要使△AED∽△ABC,应添加条件是 ;(只写出一种即可). 
 ABC分成面积相等的两部分,即SⅠ=SⅡ,求AD的长.
ABC分成面积相等的两部分,即SⅠ=SⅡ,求AD的长.
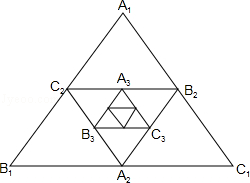

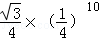
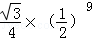
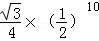





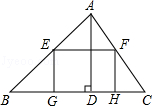
 =
= ,S四边形BCFE=8,则S△ABC=( )
,S四边形BCFE=8,则S△ABC=( )
 AB,则△ADE的周长与△ABC的周长的比为 .
AB,则△ADE的周长与△ABC的周长的比为 .