Question

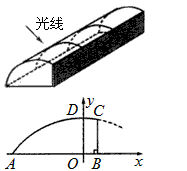
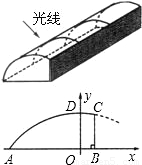
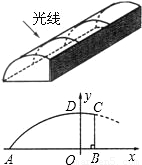
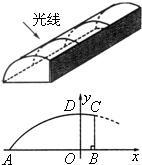26、某塑料大棚的截面如图所示，曲线部分近似看作抛物线．现测得AB=6米，最高点D到地面AB的距离DO=2.5米，点O到墙BC的距离OB=1米．借助图中的直角坐标系，回答下列问题：
（1）写出点A，B的坐标；
（2）求墙高BC．

Answer 1

分析：（1）由OB=1，AB=6，可求点A、B的坐标；
（2）要求墙高BC，可先求出抛物线的关系式．由C点的横坐标为1，代入函数关系式中可求函数y的值即墙高BC．

解答：解：（1）由题意得：
A（-5，0），B（1，0）．（2分）
（2）设y=ax²+2.5，把A（-5，0）代入
得25a+2.5=0，a=-0.1，
即y=-0.1x²+2.5．（6分）
当x=1时，y=-0.1+2.5=2.4
即墙高BC为2.4米．（8分）

点评：本题考查点的坐标的求法及二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．