Question

EF为⊙O的切线，A为切点，过点A作AP⊥EF，交⊙O的弦BC于点P，若PA=2cm，⊙O的半径为5cm，且PB：PC=2：3，则PB=________．

Answer 1

分析：根据切线的性质得出AP过圆心O，求出PR，设PB=2x，pc=3x，根据相交弦定理得出PA×PR=PB×PC，代入即可求出答案．
解答：解：∵EF切圆O于A，AP⊥EF，
∴AP过圆心O，
∵AP=2，圆O的半径是5，
∴PR=8，
设PB=2x，pc=3x，
由相交弦定理得：PA×PR=PB×PC，
∴2×8=2x•3x，
∴x=，
∴PB=2×=，
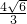故答案为：．
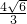点评：本题主要考查对切线的性质，相交弦定理，解一元二次方程等知识点的理解和掌握，能根据题意得出2×8=2x•3x是解此题的关键．