题目内容
 如图,AB=AC,∠BAC=110°,AB的垂直平分线交BC于点D,那么∠ADC=
如图,AB=AC,∠BAC=110°,AB的垂直平分线交BC于点D,那么∠ADC=
- A.50°
- B.60°
- C.70°
- D.80°
C
分析:先根据等腰三角形内角和定理得出∠B的度数,再由中垂线的知识得出△ABD为等腰直角三角形,可得出∠BAD的度数,根据三角形的一个外角等于与其不相邻的两内角和,即可得出∠ADC的度数.
解答:根据题意,在△ABC中,AB=AC,∠BAC=110°,
∴∠B=35°,
又AB的垂直平分线交BC于点D,
∴∠BAD=∠B=35°,
在△BAD中,∠ADC=∠A=∠BAD=70°,
∴∠ADC=70°.
故答案选C.
点评:本题主要考查的是等腰三角形的性质及三角形内角和定理和三角形的一个外角等于与其不相邻的两内角和.做题时,要结合图形,选择方法.
分析:先根据等腰三角形内角和定理得出∠B的度数,再由中垂线的知识得出△ABD为等腰直角三角形,可得出∠BAD的度数,根据三角形的一个外角等于与其不相邻的两内角和,即可得出∠ADC的度数.
解答:根据题意,在△ABC中,AB=AC,∠BAC=110°,
∴∠B=35°,
又AB的垂直平分线交BC于点D,
∴∠BAD=∠B=35°,
在△BAD中,∠ADC=∠A=∠BAD=70°,
∴∠ADC=70°.
故答案选C.
点评:本题主要考查的是等腰三角形的性质及三角形内角和定理和三角形的一个外角等于与其不相邻的两内角和.做题时,要结合图形,选择方法.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 24、如图,AB=AC=AD.
24、如图,AB=AC=AD. (2012•虹口区一模)已知:如图,AB=AC,∠DAE=∠B.
(2012•虹口区一模)已知:如图,AB=AC,∠DAE=∠B.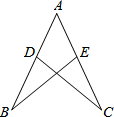 (2013•来宾)如图,AB=AC,D,E分别是AB,AC上的点,下列条件中不能证明△ABE≌△ACD的是
(2013•来宾)如图,AB=AC,D,E分别是AB,AC上的点,下列条件中不能证明△ABE≌△ACD的是 如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC的度数.
如图,AB=AC,∠C=67°,AB的垂直平分线EF交AC于点D,求∠DBC的度数. 如图,AB=AC=10,∠A=40°,AB的垂直平分线MN交AC于点D,求:
如图,AB=AC=10,∠A=40°,AB的垂直平分线MN交AC于点D,求: