题目内容
已知⊙O是△ABC的内切圆，切点为D、E、F，设∠A=x，∠EDF=y，求y与x的函数关系式．
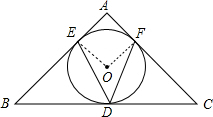解：连OE，OF．如图，则OE⊥AB，OF⊥AC，
因此∠A+∠EOF=180°；
又∵∠EOF=2∠EDF，
∴∠A+2∠EDF=180°，即x+2y=180°，
∴y=90°+
x．分析：连OE，OF，首先得到∠A和∠EOF的关系，再由同弧所对圆心角是它所对的圆周角2倍得到∠EOF与∠EDF的关系，最后确定x，y的关系式．
点评：熟悉三角形的内切圆的性质和圆周角定理．
练习册系列答案
相关题目
已知α，β是△ABC的两个角，且sinα，tanβ是方程2x2-3x+1=0的两根，则△ABC是（ ）
| A、锐角三角形 | B、直角三角形或钝角三角形 | C、钝角三角形 | D、等边三角形 |
9、如图，已知AD是△ABC的角平分线，CE⊥AD，垂足O，CE交AB于E，则下列命题：①AE=AC，②CO=OE，③∠AEO=∠ACO，④∠B=∠ECB．其中正确的是（ ）已知O是△ABC的外心，∠ABC=60°，AC=4，则△ABC外接圆的半径是（ ）
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
F⊥AB于F，且CE=CF．
如图，已知BE是△ABC的高，AE=BE，