题目内容
已知:在△ABC中,AB=AC,∠A=40°,O为边BC的中点,把△ABC绕点O顺时针旋转m(0<m<180)度后,如果点B恰好落在初始△ABC的边上,那么m=________.
40°或140°
分析:分为点B落在AB上,点B落在AC上两种情况,根据等腰三角形的性质分别求m的值.
解答: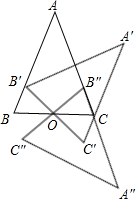 解:∵在△ABC中,AB=AC,∠A=40°,
解:∵在△ABC中,AB=AC,∠A=40°,
∴∠B=∠ACB= (180°-∠A)=70°,
(180°-∠A)=70°,
①当△ABC绕O点旋转到△A′B′C′位置时,B′落在AB上,
则OB=OB′,旋转角∠BOB′=m=180°-2∠B=40°,
②当△ABC绕O点旋转到△A″B″C″位置时,B″落在AC上,
同理可得∠B″OC=40°,
旋转角∠BOB″=m=180°-∠B″OC=140°,
故答案为:40°或140°.
点评:本题考查了等腰三角形的性质及旋转的性质.关键是根据旋转的方向,确定B点的两个位置,根据等腰三角形的性质求解.
分析:分为点B落在AB上,点B落在AC上两种情况,根据等腰三角形的性质分别求m的值.
解答:
 解:∵在△ABC中,AB=AC,∠A=40°,
解:∵在△ABC中,AB=AC,∠A=40°,∴∠B=∠ACB=
 (180°-∠A)=70°,
(180°-∠A)=70°,①当△ABC绕O点旋转到△A′B′C′位置时,B′落在AB上,
则OB=OB′,旋转角∠BOB′=m=180°-2∠B=40°,
②当△ABC绕O点旋转到△A″B″C″位置时,B″落在AC上,
同理可得∠B″OC=40°,
旋转角∠BOB″=m=180°-∠B″OC=140°,
故答案为:40°或140°.
点评:本题考查了等腰三角形的性质及旋转的性质.关键是根据旋转的方向,确定B点的两个位置,根据等腰三角形的性质求解.

练习册系列答案
相关题目
 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.