题目内容
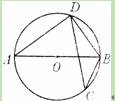
(2011•成都)如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点.
(1)若BK= KC,求
KC,求 的值;
的值;
(2)连接BE,若BE平分∠ABC,则当AE=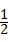 AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=
AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE= AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
解:(1)∵BK= KC,∴
KC,∴ =
= ,
,
又∵CD∥AB,
∴△KCD∽△KBA,∴ =
= =
= ;
;
(2)当BE平分∠ABC,AE=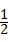 AD时,AB=BC+CD.
AD时,AB=BC+CD.
证明:取BD的中点为F,连接EF交BC与G点,
由中位线定理,得EF∥AB∥CD,∴G为BC的中点,∠GEB=∠EBA,
又∠EBA=∠GBE,∴∠GEB=∠GBE,
∴EG=BG=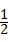 BC,而GF=
BC,而GF=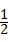 CD,EF=
CD,EF=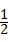 AB,
AB,
∵EF=EG+GF,∴AB=BC+CD;
当AE= AD(n>2)时,BC+CD=(n﹣1)AB.
AD(n>2)时,BC+CD=(n﹣1)AB.
解析

练习册系列答案
相关题目



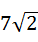 ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.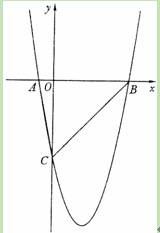
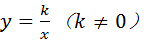 的图象经过点(
的图象经过点(