题目内容
9、如图，将两根钢条AA′、BB′的中点O连在一起，使AA′、BB′可以绕点O自由转动，就做成了一个测量工件，则A′B′的长等于内槽宽AB，则判定△OAB≌△OA′B′的理由是（ ）分析：因为AA′、BB′的中点O连在一起，因此OA=OA′，OB=OB′，还有对顶角相等，所以用的判定定理是边角边．
解答：解：∵AA′、BB′的中点O连在一起，
∴OA=OA′，OB=OB′，
∵∠AOB=∠A′OB′，
∴△OAB≌△OA′B′．
所以用的判定定理是边角边．
故选C．
∴OA=OA′，OB=OB′，
∵∠AOB=∠A′OB′，
∴△OAB≌△OA′B′．
所以用的判定定理是边角边．
故选C．
点评：本题考查全等三角形的判定定理，关键知道是怎么证明的全等，然后找到用的是那个判定定理．
练习册系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
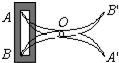4、如图，将两根钢条AA′、BB′的中点O连在一起，使AA′、BB′可以绕着点O自由转动，就做成了一个测量工件，由三角形全等得出A′B′的长等于内槽宽AB；那么判定△OAB≌△OA′B′的理由是（ ）
如图，将两根钢条AA′、BB′的中点 O连在一起，使AA′、BB′能绕着点O自由转动，就做成了一个测量工具，由三角形全等可知A′B′的长等于内槽宽AB，那么判定△OAB≌△OA′B′的理由是（ ）
