题目内容
如图,已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE;
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并写出推理过程;
(3)若将锐角△ABC变为钝角△ABC,如图,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.
(1)求证:MN⊥DE;
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并写出推理过程;
(3)若将锐角△ABC变为钝角△ABC,如图,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.

分析:(1)连接DM、ME,根据直角三角形斜边上的中线等于斜边的一半可得DM=
BC,ME=
BC,从而得到DM=ME,再根据等腰三角形三线合一的性质证明;
(2)根据三角形的内角和定理可得∠ABC+∠ACB=180°-∠A,再根据等腰三角形两底角相等表示出∠BMD+∠CME,然后根据平角等于180°表示出∠DME,整理即可得解;
(3)根据三角形的内角和定理可得∠ABC+∠ACB=180°-∠A,再根据等腰三角形两底角相等和三角形的一个外角等于与它不相邻的两个内角的和表示出∠BME+∠CME,然后根据平角等于180°表示出∠DME,整理即可得解.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据三角形的内角和定理可得∠ABC+∠ACB=180°-∠A,再根据等腰三角形两底角相等表示出∠BMD+∠CME,然后根据平角等于180°表示出∠DME,整理即可得解;
(3)根据三角形的内角和定理可得∠ABC+∠ACB=180°-∠A,再根据等腰三角形两底角相等和三角形的一个外角等于与它不相邻的两个内角的和表示出∠BME+∠CME,然后根据平角等于180°表示出∠DME,整理即可得解.
解答:解:(1)如图,连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点,
∴DM=
BC,ME=
BC,
∴DM=ME
又∵N为DE中点,
∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°-∠A,
∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°-2∠ABC)+(180°-2∠ACB),
=360°-2(∠ABC+∠ACB),
=360°-2(180°-∠A),
=2∠A,
∴∠DME=180°-2∠A;
(3)结论(1)成立,
结论(2)不成立,
理由如下:在△ABC中,∠ABC+∠ACB=180°-∠A,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC,
=2(180°-∠A),
=360°-2∠A,
∴∠DME=180°-(360°-2∠A),
=2∠A-180°.
∵CD、BE分别是AB、AC边上的高,M是BC的中点,
∴DM=
| 1 |
| 2 |
| 1 |
| 2 |
∴DM=ME
又∵N为DE中点,
∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°-∠A,
∵DM=ME=BM=MC,

∴∠BMD+∠CME=(180°-2∠ABC)+(180°-2∠ACB),
=360°-2(∠ABC+∠ACB),
=360°-2(180°-∠A),
=2∠A,
∴∠DME=180°-2∠A;
(3)结论(1)成立,
结论(2)不成立,
理由如下:在△ABC中,∠ABC+∠ACB=180°-∠A,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC,
=2(180°-∠A),
=360°-2∠A,
∴∠DME=180°-(360°-2∠A),
=2∠A-180°.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形两底角相等的性质,三角形的内角和定理,整体思想的利用是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目




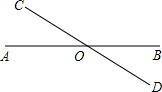 如图,已知直线AB和CD相交于点O(∠AOC为锐角)
如图,已知直线AB和CD相交于点O(∠AOC为锐角) 如图,已知直线AB和CD相交于点O(∠AOC为锐角)
如图,已知直线AB和CD相交于点O(∠AOC为锐角)