题目内容
如图，由边长分别为8厘米，10厘米，12厘米的三个不同的正方形组成的图形，现请你经过C点沿一条直线把它剪开，使整个图形的面积被平均分成2份．在下面的图形中画出直线，并指出具体位置．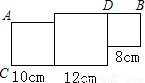
【答案】分析：过C作直线CE交BD于点E，使三个正方形的面积分为相等的两部分，再延长KF、CA两直线相交于点K，设BE=x，再根据两部分面积相等即可求出x的值，进而可确定直线CE的位置．
解答：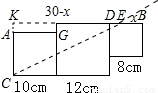
解：如图所示，过C作直线CE交BD于点E，使三个正方形的面积分为相等的两部分，再延长KF、CA两直线相交于点K，设BE=x，
则SAGKF=2×10=20cm，
∵直线CE将三个正方形分为面积相等的两部分，
∴
（30-x）×12-20=
（10×10+12×12+8×8），
解得x=1．
∴E点在距离点B1厘米处．
点评：本题考查的是面积及等积变换，解答此题的关键是根据两部分面积相等列出关于x的方程，求出x的值即可确定直线的具体位置．
解答：
解：如图所示，过C作直线CE交BD于点E，使三个正方形的面积分为相等的两部分，再延长KF、CA两直线相交于点K，设BE=x，则SAGKF=2×10=20cm，
∵直线CE将三个正方形分为面积相等的两部分，
∴
（30-x）×12-20=（10×10+12×12+8×8），解得x=1．
∴E点在距离点B1厘米处．
点评：本题考查的是面积及等积变换，解答此题的关键是根据两部分面积相等列出关于x的方程，求出x的值即可确定直线的具体位置．
练习册系列答案
相关题目
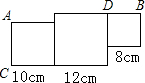如图，由边长分别为8厘米，10厘米，12厘米的三个不同的正方形组成的图形，现请你经过C点沿一条直线把它剪开，使整个图形的面积被平均分成2份．在下面的图形中画出直线，并指出具体位置．
如图，是由边长分别为2a和a的两个正方形组成，闭上眼睛，由针随意扎这个图形，小孔出现在阴影部分的概率是
）拼成一个六边形，由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形，其面积可计算出为 ；由于所围成的小六边形的边长都是 ，其面积为 ，由此可得
),先画出这个正三角形,再推出
边形吗?如果能,试写出∠A和三角形的面积
的表达式;如果不能,请简要说明理由.