题目内容
设四边形ABCD与四边形A1B1C1D1是相似的图形,且A与A1、B与B1、C与C1是对应点,已知AB=12,BC=18,CD=18,AD=9,A1B1=8,求四边形A1B1C1D1的周长.
解:∵四边形ABCD与四边形A1B1C1D1是相似的图形
∴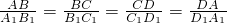
又∵AB=12,BC=18,CD=18,AD=9,A1B1=8
∴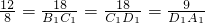
∴B1C1=12,C1D1=12,D1A1=6
∴四边形A1B1C1D1的周长=8+12+12+6=38.
分析:四边形ABCD与四边形A1B1C1D1是相似的图形,则根据相似多边形对应边的比相等,就可求得A1B1C1D1的其它边的长,就可求得周长.
点评:本题考查相似多边形的性质,相似多边形对应边之比相等.
∴
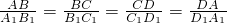
又∵AB=12,BC=18,CD=18,AD=9,A1B1=8
∴
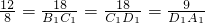
∴B1C1=12,C1D1=12,D1A1=6
∴四边形A1B1C1D1的周长=8+12+12+6=38.
分析:四边形ABCD与四边形A1B1C1D1是相似的图形,则根据相似多边形对应边的比相等,就可求得A1B1C1D1的其它边的长,就可求得周长.
点评:本题考查相似多边形的性质,相似多边形对应边之比相等.

练习册系列答案
相关题目
 的距离为x,△PAB的面积为y,y与x的函数图象如图所示.
的距离为x,△PAB的面积为y,y与x的函数图象如图所示. (2012•营口)如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.
(2012•营口)如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.
 如图,四边形ABCD是任意四边形,过点A,C作BD的平行线,再过点B、D作AC的平行线,设四条直线的交点为P,Q,M,N.
如图,四边形ABCD是任意四边形,过点A,C作BD的平行线,再过点B、D作AC的平行线,设四条直线的交点为P,Q,M,N.