题目内容
四边形ABCD中,AB∥CD,若再增加一个条件________,则可使四边形ABCD为平行四边形
AB=CD (AD∥BC)
试题分析:已知AB∥CD,根据两组对边分别相等的四边形是平行四边形,添加AD∥BC;或根据一组对边平行且相等的四边形是平行四边形,添加AB=CD.
∵AB=CD,
∴当AD=BC,(两组对边分别相等的四边形是平行四边形.)
或AB∥CD(一组对边平行且相等的四边形是平行四边形.)时,
四边形ABCD是平行四边形.
考点:本题考查了平行四边形的判定
点评:解答本题的关键是熟练掌握平行四边形的五种判定方法:
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)一组对边平行且相等的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)对角线互相平分的四边形是平行四边形.
试题分析:已知AB∥CD,根据两组对边分别相等的四边形是平行四边形,添加AD∥BC;或根据一组对边平行且相等的四边形是平行四边形,添加AB=CD.
∵AB=CD,
∴当AD=BC,(两组对边分别相等的四边形是平行四边形.)
或AB∥CD(一组对边平行且相等的四边形是平行四边形.)时,
四边形ABCD是平行四边形.
考点:本题考查了平行四边形的判定
点评:解答本题的关键是熟练掌握平行四边形的五种判定方法:
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)一组对边平行且相等的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)对角线互相平分的四边形是平行四边形.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.
23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.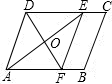 如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )
如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( ) 17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形:
17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形: 7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.
7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.