题目内容
抛物线y=-
（x+2）2-4的开口向________，顶点坐标________，对称轴________，x________时，y随x的增大而增大，x________时，y随x的增大而减小．
下 （-2，4） x=-2 ＜-2 ＞-2
分析：已知抛物线解析式为顶点式，可确定对称轴、顶点坐标，二次项系数为负数，可确定开口方向、增减性及最大值．
解答：∵y=-（x+2）2-4为抛物线的顶点式，
∴图象开口向下，
顶点坐标是（-2，4），
抛物线的对称轴是x=-2，
当x＜-2时，y随x的增大而增大，
当x＞-2时，y随x的增大而减小，
故答案为：下，（-2，-4），x=-2，＜-2，＞-2．
点评：本题考查了抛物线的顶点式与抛物线的性质之间的关系，关键是明确抛物线的顶点坐标及开口方向．
分析：已知抛物线解析式为顶点式，可确定对称轴、顶点坐标，二次项系数为负数，可确定开口方向、增减性及最大值．
解答：∵y=-
（x+2）2-4为抛物线的顶点式，∴图象开口向下，
顶点坐标是（-2，4），
抛物线的对称轴是x=-2，
当x＜-2时，y随x的增大而增大，
当x＞-2时，y随x的增大而减小，
故答案为：下，（-2，-4），x=-2，＜-2，＞-2．
点评：本题考查了抛物线的顶点式与抛物线的性质之间的关系，关键是明确抛物线的顶点坐标及开口方向．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
A和C，和x轴的另一个交点为B．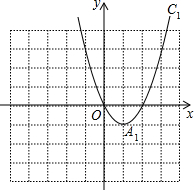
已知抛物线C1：y=x2-2x的图象如图所示，把C1的图象沿y轴翻折，得到抛物线C2的图象，抛物线C1与抛物线C2的图象合称图象C3．