题目内容
 如图,等腰三角形ABC,AB=AC,以AB为直径作圆O分别交AC、BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:①
如图,等腰三角形ABC,AB=AC,以AB为直径作圆O分别交AC、BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:① ,②FD是⊙O的切线;③∠C=∠DFB;④E是△BDF的内心.
,②FD是⊙O的切线;③∠C=∠DFB;④E是△BDF的内心.
其中一定正确的结论是
- A.①②③
- B.①②④
- C.①③④
- D.②③④
B
分析:首先利用三角形的中位线定理证明OE∥AC,然后证得∠BOE=∠EOD可得:① ,再证明△FDO≌△FBO,可以得到DF是圆的切线;利用等腰三角形的性质:等边对等角即可判断③的正误;然后根据角相等证明E在∠FAB和∠FBD的角平分线上和E在∠FBD的平分线上,利用内心的定义可得到④的正误.
,再证明△FDO≌△FBO,可以得到DF是圆的切线;利用等腰三角形的性质:等边对等角即可判断③的正误;然后根据角相等证明E在∠FAB和∠FBD的角平分线上和E在∠FBD的平分线上,利用内心的定义可得到④的正误.
解答:连接AE,DO,
∵AB是直径,
∴∠AEB=90°,
∴AE⊥BC,
又∵AB=AC,
∴BE=CE,
又∵OA=OB,
∴OE∥AC,
∴∠BOE=∠BAC,∠EOD=∠ADO,
∵∠BAC=∠ADO,
∴∠BOE=∠EOD,
∴ ,
,
故①正确;
在△FDO和△FBO中,
∵ ,
,
∴△FDO≌△FBO(SAS),
∴∠ODF=∠OBF=90°,
即△FDO是直角三角形,DF是⊙O的切线.
故②正确;
设∠C=x°,则∠CAB=(180-2x)°,
则在直角△ABD中,∠ABD=90°-(180-2x)°=(2x-90)°,
∵BF是切线,则∠ABF=90°,
∴∠DBF=90°-∠ABD=90°-(2x-90)°=(180-2x)°,
在等腰△BDF中,∠DFB=180°-2∠DBF=180°-2(180-2x)°=(4x-180)°,
而4x-180与x不一定相等,故③不正确.
连接DE,DB,
∵FD、FB是圆的切线,
∴FD=FB,
又∵OB=OD
∴OF是BD的中垂线,
∴E在∠FBD的平分线上,
∵ ,
,
∴∠FBE=∠CBD,∠FDE=∠DEB,
∴E在∠FDB和∠FBD的角平分线上,
∴E是△BFD的内心,故④正确.
故选:B.
点评:此题主要考查了三角形的内心、外心以及切线的判定,解答的关键是正确证得DF是圆的切线.
分析:首先利用三角形的中位线定理证明OE∥AC,然后证得∠BOE=∠EOD可得:①
 ,再证明△FDO≌△FBO,可以得到DF是圆的切线;利用等腰三角形的性质:等边对等角即可判断③的正误;然后根据角相等证明E在∠FAB和∠FBD的角平分线上和E在∠FBD的平分线上,利用内心的定义可得到④的正误.
,再证明△FDO≌△FBO,可以得到DF是圆的切线;利用等腰三角形的性质:等边对等角即可判断③的正误;然后根据角相等证明E在∠FAB和∠FBD的角平分线上和E在∠FBD的平分线上,利用内心的定义可得到④的正误.解答:连接AE,DO,
∵AB是直径,
∴∠AEB=90°,
∴AE⊥BC,
又∵AB=AC,
∴BE=CE,
又∵OA=OB,
∴OE∥AC,
∴∠BOE=∠BAC,∠EOD=∠ADO,
∵∠BAC=∠ADO,
∴∠BOE=∠EOD,
∴
 ,
,故①正确;
在△FDO和△FBO中,
∵
 ,
,∴△FDO≌△FBO(SAS),
∴∠ODF=∠OBF=90°,
即△FDO是直角三角形,DF是⊙O的切线.
故②正确;
设∠C=x°,则∠CAB=(180-2x)°,
则在直角△ABD中,∠ABD=90°-(180-2x)°=(2x-90)°,
∵BF是切线,则∠ABF=90°,
∴∠DBF=90°-∠ABD=90°-(2x-90)°=(180-2x)°,
在等腰△BDF中,∠DFB=180°-2∠DBF=180°-2(180-2x)°=(4x-180)°,
而4x-180与x不一定相等,故③不正确.
连接DE,DB,
∵FD、FB是圆的切线,
∴FD=FB,
又∵OB=OD

∴OF是BD的中垂线,
∴E在∠FBD的平分线上,
∵
 ,
,∴∠FBE=∠CBD,∠FDE=∠DEB,
∴E在∠FDB和∠FBD的角平分线上,
∴E是△BFD的内心,故④正确.
故选:B.
点评:此题主要考查了三角形的内心、外心以及切线的判定,解答的关键是正确证得DF是圆的切线.

练习册系列答案
相关题目
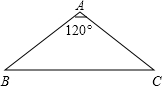 如图,等腰三角形ABC的顶角为120°,底边BC=
如图,等腰三角形ABC的顶角为120°,底边BC=
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
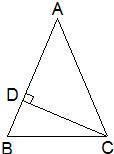 9、如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于( )
9、如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于( ) (1)他们的说法合理吗?为什么?
(1)他们的说法合理吗?为什么?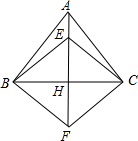 如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,
如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,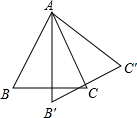 如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转
如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转