题目内容
已知如图1,Rt△ABC和Rt△ADE的直角边AC和AE重叠在一起,AD=AE,∠B=30°,∠DAE=∠ACB=90°.(1)如图1,填空:∠BAD=
| BC | CD |
(2)如图2,将△ADE绕点A顺时针旋转,使AE到AB边上,∠ACH=∠BCH,连接BH,求∠CBH的度数;
(3)如图3,点P是BE上一点,过A、E两点分别作AN⊥PC、EM⊥PC,垂足分别为N、M,若EM=2,AN=5,求△AND的面积.
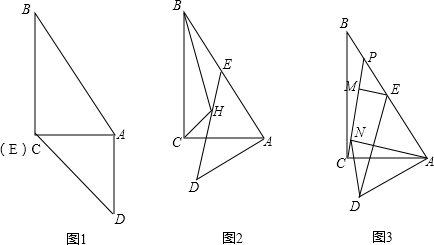
分析:(1)如图1,由三角形内角和定理求得∠BAC=60°,则∠BAD=∠BAC+90°=150°;把BC、CD的长度均以AC表示,通过约分可以求得
的值;
(2)如图2,连接CE、AH.先证等边△ACE得AE=AC,∠AEC=∠ACE=60°.而∠AEH=∠ACH=45°,易推知∠HEC=∠HCE=15°,所以HE=HC.再证△AEH≌△ACH(SAS),由AH平分∠BAC、CH平分∠ACB,得到BH平分∠ABC,则∠CBH=15°;
(3)如图3,过点E作EF⊥AN于点F,过点D作DG⊥AN于点G,可得矩形MEFN.可证△AEF≌△DAG.则DG=AF=AN-EM=5-2=3.所以S△AND=
AN•DG=
×5×3=
.
| BC |
| CD |
(2)如图2,连接CE、AH.先证等边△ACE得AE=AC,∠AEC=∠ACE=60°.而∠AEH=∠ACH=45°,易推知∠HEC=∠HCE=15°,所以HE=HC.再证△AEH≌△ACH(SAS),由AH平分∠BAC、CH平分∠ACB,得到BH平分∠ABC,则∠CBH=15°;
(3)如图3,过点E作EF⊥AN于点F,过点D作DG⊥AN于点G,可得矩形MEFN.可证△AEF≌△DAG.则DG=AF=AN-EM=5-2=3.所以S△AND=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
解答: 解:(1)如图1,∵∠ACB=90°,∠B=30°,
解:(1)如图1,∵∠ACB=90°,∠B=30°,
∴∠BAC=60°.
又∵∠DAE=90°,
∴∠BAD=∠BAC+90°=150°;
在Rt△ABC中,BC=AC•tan60°=
AC.
在Rt△ADE中,AD=AC,则CD=
AC,
∴
=
=
.
故答案是:150°,
;
(2)如图2,连接CE、AH.
∵AC=AE,∠CAE=60°,
∴△ACE是等边三角形,
∴AE=AC,∠AEC=∠ACE=60°.
由∵∠AEH=∠ACH=45°,
∴∠HEC=∠HCE=15°,
∴HE=HC.
在△AEH与△ACH中,
,
∴△AEH≌△ACH(SAS),
∴∠EAH=∠CAH,即AH平分∠BAC.
又∵∠ACH=∠BCH,即CH平分∠ACB,
∴BH平分∠ABC,则∠CBH=15°;
(3)如图3,过点E作EF⊥AN于点F,过点D作DG⊥AN于点G.
∵AN⊥PC、EM⊥PC,
∴四边形MEFN是矩形.可证△AEF≌△DAG.
∴DG=AF=AN-EM=5-2=3.
∴S△AND=
AN•DG=
×5×3=
.
 解:(1)如图1,∵∠ACB=90°,∠B=30°,
解:(1)如图1,∵∠ACB=90°,∠B=30°,∴∠BAC=60°.
又∵∠DAE=90°,
∴∠BAD=∠BAC+90°=150°;
在Rt△ABC中,BC=AC•tan60°=
| 3 |
在Rt△ADE中,AD=AC,则CD=
| 2 |
∴
| BC |
| CD |
| ||
|
| ||
| 2 |
故答案是:150°,
| ||
| 2 |
(2)如图2,连接CE、AH.
∵AC=AE,∠CAE=60°,
∴△ACE是等边三角形,
∴AE=AC,∠AEC=∠ACE=60°.
由∵∠AEH=∠ACH=45°,
∴∠HEC=∠HCE=15°,
∴HE=HC.
在△AEH与△ACH中,
|
∴△AEH≌△ACH(SAS),
∴∠EAH=∠CAH,即AH平分∠BAC.
又∵∠ACH=∠BCH,即CH平分∠ACB,
∴BH平分∠ABC,则∠CBH=15°;
(3)如图3,过点E作EF⊥AN于点F,过点D作DG⊥AN于点G.
∵AN⊥PC、EM⊥PC,
∴四边形MEFN是矩形.可证△AEF≌△DAG.
∴DG=AF=AN-EM=5-2=3.
∴S△AND=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
点评:本题考查了几何变换综合题.其中涉及到了图形的旋转,全等三角形的判定与性质,三角形内角和定理以及三角形的面积计算.图形旋转时,旋转前、后的图形全等.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 已知如图,在Rt△ABC中,∠C=90°,D是BC中点,DE⊥AB,垂足为E,∠B=30°,AE=7.求:DE的长.
已知如图,在Rt△ABC中,∠C=90°,D是BC中点,DE⊥AB,垂足为E,∠B=30°,AE=7.求:DE的长.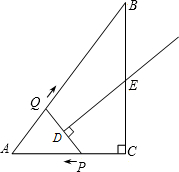 同时出发,当点P到达点A时停止运动,点Q也随之停止.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.设点P、Q运动的时间是t秒(t>0).
同时出发,当点P到达点A时停止运动,点Q也随之停止.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.设点P、Q运动的时间是t秒(t>0). 已知如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,求AB的长.
已知如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,求AB的长. 已知如图,在Rt△ABC中,∠B=90°,AB=3,AC=5.将△ABC折叠使C与A重合,折痕为DE,求BE的长.
已知如图,在Rt△ABC中,∠B=90°,AB=3,AC=5.将△ABC折叠使C与A重合,折痕为DE,求BE的长.