题目内容
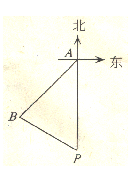
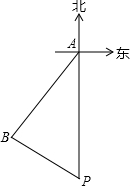 已知,如图,渔船原来应该从A点向正南方向行驶回到港口P,但由于受到海风的影响,渔船向西南方向行驶去,行驶了240千米后到达B点,此时发现港口P在渔船的南偏东60°的方向上,问渔船此时距港口P多远?(结果精确到0.1千米,参考数据:
已知,如图,渔船原来应该从A点向正南方向行驶回到港口P,但由于受到海风的影响,渔船向西南方向行驶去,行驶了240千米后到达B点,此时发现港口P在渔船的南偏东60°的方向上,问渔船此时距港口P多远?(结果精确到0.1千米,参考数据:| 2 |
| 3 |
| 5 |
| 6 |
分析:由已知条件渔船向西南方向行驶去,行驶了240千米后到达B点,即∠BAD=45°,由到达B点时发现港口P在渔船的南偏东60°的方向上,可以得到∠BPD=60°,过点B作BD⊥AP于点D,再利用三角函数关系,可求出BP长度.
解答: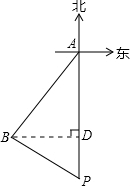 解:过点B作BD⊥AP于点D,
解:过点B作BD⊥AP于点D,
在Rt△ABD中,BD=ABsin45°=240×
=120
,
在Rt△BDP中,sin60°=
,BP=
=80
≈196.0
答:距港口约为196.0千米.
 解:过点B作BD⊥AP于点D,
解:过点B作BD⊥AP于点D,在Rt△ABD中,BD=ABsin45°=240×
| ||
| 2 |
| 2 |
在Rt△BDP中,sin60°=
| BD |
| BP |
| BD |
| sin60° |
| 6 |
≈196.0
答:距港口约为196.0千米.
点评:此题主要考查了方位角问题,正确确定方位角的度数,是解决问题的关键.

练习册系列答案
相关题目
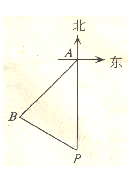
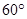 的方向上,问渔船此时距港口P多远?(结果精确到0.1千米,参考数据:
的方向上,问渔船此时距港口P多远?(结果精确到0.1千米,参考数据: ,
,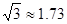 ,
,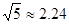 ,
, )
)
 的方向上,问渔船此时距港口P多远?(结果精确到0.1千米,参考数据:
的方向上,问渔船此时距港口P多远?(结果精确到0.1千米,参考数据: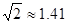 ,
,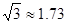 ,
,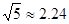 ,
,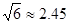 )
)
 的方向上,问渔船此时距港口P多远?(结果精确到0.1千米,参考数据:
的方向上,问渔船此时距港口P多远?(结果精确到0.1千米,参考数据: ,
, ,
, ,
, )
)