题目内容
(2009•铁岭)如图所示,已知AB是半圆O的直径,弦CD∥AB,AB=10,CD=6,E是AB延长线上一点,BE= .判断直线DE与半圆O的位置关系,并证明你的结论.
.判断直线DE与半圆O的位置关系,并证明你的结论.
【答案】分析:直线DE与半圆O相切.连接OD,作OF⊥CD于点F,作DG⊥OE于点G.通过勾股定理求得OF的长,由已知可得到四边形OFDG是矩形,从而便可求得DG,GE的长,再通过勾股定理判定CD⊥DE,从而证明得到直线DE与半圆O相切.
解答: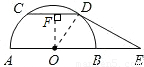 解:直线DE与半圆O相切.(1分)
解:直线DE与半圆O相切.(1分)
证法一:
连接OD,作OF⊥CD于点F.
∵CD=6,
∴DF= CD=3.(2分)
CD=3.(2分)
∵OE=OB+BE=5+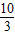 =
=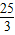 .(3分)
.(3分)
∴ ,
,
∴ .(6分)
.(6分)
∵CD∥AB,
∴∠CDO=∠DOE.(7分)
∴△DOF∽△OED,(8分)
∴∠ODE=∠OFD=90°,
∴OD⊥DE,
∴直线DE与半圆O相切.(10分)
证法二:连接OD,作OF⊥CD于点F,作DG⊥OE于点G.
∵CD=6,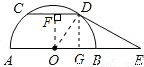
∴DF= CD=3.
CD=3.
在Rt△ODF中,OF=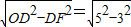 =4,(3分)
=4,(3分)
∵CD∥AB,DG⊥AB,OF⊥CD,
∴四边形OFDG是矩形,
∴DG=OF=4,OG=DF=3.
∵OE=OB+BE=5+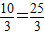 ,GE=OE-OG=
,GE=OE-OG=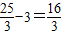 ,(5分)
,(5分)
在Rt△DGE中,DE=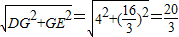 .
.
∵ ,
,
∴OD2+DE2=OE2,(8分)
∴CD⊥DE.
∴直线DE与半圆O相切.(10分)
点评:本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.
解答:
 解:直线DE与半圆O相切.(1分)
解:直线DE与半圆O相切.(1分)证法一:
连接OD,作OF⊥CD于点F.
∵CD=6,
∴DF=
 CD=3.(2分)
CD=3.(2分)∵OE=OB+BE=5+
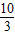 =
=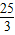 .(3分)
.(3分)∴
 ,
,∴
 .(6分)
.(6分)∵CD∥AB,
∴∠CDO=∠DOE.(7分)
∴△DOF∽△OED,(8分)
∴∠ODE=∠OFD=90°,
∴OD⊥DE,
∴直线DE与半圆O相切.(10分)
证法二:连接OD,作OF⊥CD于点F,作DG⊥OE于点G.
∵CD=6,

∴DF=
 CD=3.
CD=3.在Rt△ODF中,OF=
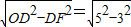 =4,(3分)
=4,(3分)∵CD∥AB,DG⊥AB,OF⊥CD,
∴四边形OFDG是矩形,
∴DG=OF=4,OG=DF=3.
∵OE=OB+BE=5+
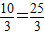 ,GE=OE-OG=
,GE=OE-OG=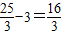 ,(5分)
,(5分)在Rt△DGE中,DE=
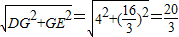 .
.∵
 ,
,∴OD2+DE2=OE2,(8分)
∴CD⊥DE.
∴直线DE与半圆O相切.(10分)
点评:本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目