题目内容
如图，在⊙O中，
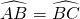，∠BAC=60°，则∠AOB：∠ABC：∠ACO等于
- A.3：2：1
- B.4：3：2
- C.4：2：1
- D.5：3：2
C
分析：由已知条件可判定三角形ABC为等边三角形，进而求出∠AOB、∠ABC、∠ACO的度数，再求比值即可．
解答：∵在⊙O中，，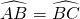
∴AB=AC，
∵∠BAC=60°，
∴△ABC为等边三角形，
∴∠ABC=60°，
∴∠AOB=120°，∠ACO=30°，
∴∠AOB：∠ABC：∠ACO=120：60：30=4：2：1．
故选C．
点评：本题考查了圆周角定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等以及推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
分析：由已知条件可判定三角形ABC为等边三角形，进而求出∠AOB、∠ABC、∠ACO的度数，再求比值即可．
解答：∵在⊙O中，
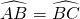，∴AB=AC，
∵∠BAC=60°，
∴△ABC为等边三角形，
∴∠ABC=60°，
∴∠AOB=120°，∠ACO=30°，
∴∠AOB：∠ABC：∠ACO=120：60：30=4：2：1．
故选C．
点评：本题考查了圆周角定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等以及推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
练习册系列答案
相关题目
19、如图，在△ABC中，CD⊥AB于D，FG⊥AB于G，ED∥BC，试说明∠1=∠2，以下是证明过程，请填空：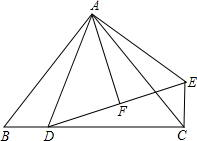
如图，在△ABC中，已知AB=AC，∠BAC=90°，D是BC上一点，EC⊥BC，EC=BD，DF=FE．求证：
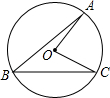如图，在⊙O中，∠ABC=40°，则∠AOC=
如图，在△ABC中，∠B，∠C的外角平分线相交于点O，若∠A=74°，则∠O=
15、如图，在△ABC中，AQ=PQ，PR=PS，PS⊥AC于S，PR⊥AB于R，则以下结论中：（1）AS=AR；（2）△BRP∽△QSP；（3）PQ∥AB中，正确的有