题目内容
解下列方程:
(1)|x+3|-|x-1|=x+1
(2)|x-1|+|x-5|=4.
解:(1)①当x≥1时,原方程可化为:x+3-(x-1)=x+1,
解得:x=3;
②当x<-3时,原方程可化为:-x-3-(1-x)=x+1,
解得:x=-5;
③当-3≤x<1时,原方程可化为:x+3+x-1=x+1,
解得:x=-1.
综上可得:方程的解为:x=3或x=-5或x=-1;
(2)
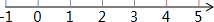
方程可理解为一个点到1和5两点的距离和,由此可得方程的解为:1≤x≤5.
分析:(1)分别讨论①x≥1,②x<-3,③-3≤x<1,再这三种情况下去掉绝对值解出方程的解即可.
(2)运用数轴上点的距离的定义可得出答案.
点评:本题考查含绝对值的一元一次方程,难度较大,注意分类讨论及数形结合思想的运用.
解得:x=3;
②当x<-3时,原方程可化为:-x-3-(1-x)=x+1,
解得:x=-5;
③当-3≤x<1时,原方程可化为:x+3+x-1=x+1,
解得:x=-1.
综上可得:方程的解为:x=3或x=-5或x=-1;
(2)
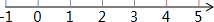
方程可理解为一个点到1和5两点的距离和,由此可得方程的解为:1≤x≤5.
分析:(1)分别讨论①x≥1,②x<-3,③-3≤x<1,再这三种情况下去掉绝对值解出方程的解即可.
(2)运用数轴上点的距离的定义可得出答案.
点评:本题考查含绝对值的一元一次方程,难度较大,注意分类讨论及数形结合思想的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目