题目内容
 甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图.根据图象解决下列问题:
甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图.根据图象解决下列问题:(1)谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2)分别求出甲、乙两人的行驶速度.
(3)看图直接说出什么时间时①甲在乙的前面;②甲与乙相遇;③甲在乙后面.
(4)求出行驶过程中路程与时间的函数关系.
分析:(1)根据函数图象解答即可;
(2)根据速度=总路程÷总时间,列式计算即可得解;
(3)根据函数图象解答即可;
(4)利用待定系数法求一次函数解析式分别求解即可.
(2)根据速度=总路程÷总时间,列式计算即可得解;
(3)根据函数图象解答即可;
(4)利用待定系数法求一次函数解析式分别求解即可.
解答:解:(1)甲先出发,先出发10分钟.乙先到达终点,先到达5分钟;
(2)甲的速度为:y甲=
=12(千米/小时),
乙的速度为:y=
=24(千米/时);
(3)①0<x<20甲在乙的前面;
②x=20甲与乙相遇;
③x>20甲在乙后面;
(4)设y甲=kx,
∵y甲=kx经过,(30,6),
∴30k=6,
解得k=
,
所以,y甲=
x;
设y乙=k1x+b,
∵y乙=k1x+b经过(10,0),(25,6),
∴
,
解得
,
所以y乙=
x-4.
(2)甲的速度为:y甲=
| 6 |
| 0.5 |
乙的速度为:y=
| 6 | ||
|
(3)①0<x<20甲在乙的前面;
②x=20甲与乙相遇;
③x>20甲在乙后面;
(4)设y甲=kx,
∵y甲=kx经过,(30,6),
∴30k=6,
解得k=
| 1 |
| 5 |
所以,y甲=
| 1 |
| 5 |
设y乙=k1x+b,
∵y乙=k1x+b经过(10,0),(25,6),
∴
|
解得
|
所以y乙=
| 2 |
| 5 |
点评:本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式以及识别函数图象的能力.

练习册系列答案
相关题目
 甲骑自行车、乙骑摩托沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图所示.根据图象可知:
甲骑自行车、乙骑摩托沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图所示.根据图象可知: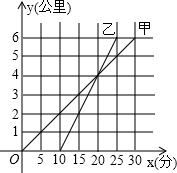 甲骑自行车、乙骑摩托沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图所示.根据图象可知:
甲骑自行车、乙骑摩托沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图所示.根据图象可知: