题目内容
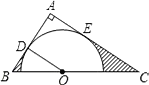
【题目】如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.
求:(1)tanC;
(2)图中两部分阴影面积的和.
【答案】解:(1)连接OE,
∵AB、AC分别切⊙O于D、E两点,
∴∠ADO=∠AEO=90°,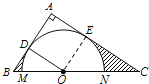
又∵∠A=90°,
∴四边形ADOE是矩形,
∵OD=OE,
∴四边形ADOE是正方形,
∴OD∥AC,OD=AD=3,
∴∠BOD=∠C,
∴在Rt△BOD中,![]() ,
,
∴![]() .
.
答:tanC=![]() .
.
(2)解:如图,设⊙O与BC交于M、N两点,
由(1)得:四边形ADOE是正方形,
∴∠DOE=90°,
∴∠COE+∠BOD=90°,
∵在Rt△EOC中,![]() ,OE=3,
,OE=3,
∴![]() ,
,
∴S扇形DOM+S扇形EON=S扇形DOE=![]() ,
,
∴S阴影=S△BOD+S△COE﹣(S扇形DOM+S扇形EON)=![]() ,
,
答:图中两部分阴影面积的和为![]() .
.
【解析】解:(1)连接![]()
∵![]() 、
、![]() 分别切
分别切![]() 于
于![]() 、
、![]() 两点
两点
∴![]()
又∵![]()
∴四边形![]() 是矩形
是矩形
∵![]()
∴四边形![]() 是正方形. .................................(2分)
是正方形. .................................(2分)
∴![]() ∥
∥![]() ,
, ![]()
∴![]()
∴在![]() 中,
中, ![]()
∴![]() . .................................(5分)
. .................................(5分)
(2)如图,设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点.由(1)得,四边形
两点.由(1)得,四边形![]() 是正方形
是正方形

∴![]()
∴![]()
∵在![]() 中,
中, ![]() ,
, ![]()
∴![]() . .................................(7分)
. .................................(7分)
∴![]()
∴![]()
∴图中两部分阴影面积的和为![]() ............ 9分
............ 9分
(1)连接![]() ,求得四边形
,求得四边形![]() 是正方形,得出AD的长,从而求得
是正方形,得出AD的长,从而求得![]()
(2)根据阴影面积等于三角形的面积减去扇形的面积求得

练习册系列答案
相关题目