Question

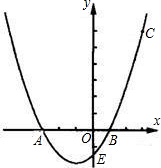如图，抛物线y=ax²+bx+c经过A（-3，0），B（1，0），C（3，6）三点，且与y轴交于点E．（1）求抛物线的解析式；
（2）若点F的坐标为（0，-

1

2

），直线BF交抛物线于另一点P，试比较△AFO与△PEF的周长的大小，并说明理由．

Answer 1

分析：（1）可根据A、B、C三点坐标，用待定系数法求出抛物线的解析式．
（2）求出两三角形的周长，就必须知道P点的坐标，可先根据B、F的坐标求出直线BF的解析式，然后联立抛物线的解析式即可求出P点坐标，然后根据A、E、F、P四点坐标求出两三角形的周长，然后判断它们的大小即可．

解答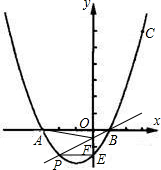：解：（1）设抛物线的解析式为y=a（x+3）（x-1），
已知抛物线过C点则有：a（3+3）（3-1）=6，
解得a=

1

2

，
∴抛物线解析式为y=

1

2

x²+x-

3

2

．

（2）∵直线BF解析式为y=

1

2

x-

1

2

，
∴列出方程组

y= 1 2 x- 1 2 y= 1 2 x2+x- 3 2

，
解得

x1=1 x2=0

，

x2=-2 y2=- 3 2

，
∴点P坐标（-2，-

3

2

）．
求出△AFO的周长为

7

2

+

37

2

，
求出△PEF的周长为3+

5

，
∴△AFO的周长大于△PEF的周长．

点评：本题主要考查了用待定系数法求二次函数解析式以及函数图象交点的求法等知识点．