Question

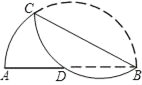
【题目】如图，在以AB为直径的半圆中，将弧BC沿弦BC折叠交AB于点D，若AD=5，DB=7．

（1）求BC的长；

（2）求圆心到BC的距离．

Answer 1

【答案】（1）；（2）圆心到BC的距离为．

【解析】（1）根据折叠的性质知：；若连接CD、AC，则∠DBC+∠BCD=∠CAD，即∠CAD=∠CDA；过C作AB的垂线，设垂足为E，则DE=AD，由此可求出BE的长，进而可在Rt△ABC中，根据射影定理求出BC的长．

（2）设圆心到BC的距离为h，利用勾股定理解答即可．

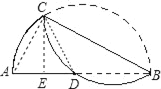
（1）连接CA、CD；

根据折叠的性质，得：；

∴∠CAB=∠CBD+∠BCD；

∵∠CDA=∠CBD+∠BCD（三角形的一个外角等于和它不相邻的两个内角的和），

∴∠CAD=∠CDA，即△CAD是等腰三角形；

过C作CE⊥AB于E，则AE=DE=2.5；

∴BE=BD+DE=9.5；

在Rt△ACB中，CE⊥AB，根据射影定理，得：

BC2=BEAB=9.5×12=114；

故BC=．

（2）设圆心到BC的距离为h，圆的半径为r=6，

由（1）知，Rt△ECB中，BE=9.5，BC=，

∴，

∵sin=，

∴h=，

故圆心到BC的距离为．