Question

已知：如下图，在△ABC中，∠ACB为直角，D，E分别是AC，AB的中点，点F在BC的延长线上，并且∠CDF=∠A．

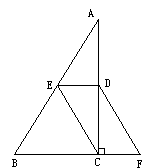
(1)求证：四边形DECF是平行四边形；

(2)若sinA=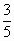，四边形EBFD的周长为66cm，求△AEC的面积．

Answer 1

答案：
解析：

(1)因为∠ACB=，E为AB的中点，D为AC的中点， 　　Rt△AED≌Rt△CED，所以AE=EC，∠1=∠A 　　又因∠CDF=∠A，所以∠1=∠CDF，EC∥DF 　　因为D是AC的中点，E是AB的中点，所以ED∥CF，四边形DECF是平行四边形． 　　(2)设ED=3x，则AE=BE=5x，所以EC=DF=5x， 　　因为DE=3x，所以CF=3x，BC=6x， 　　所以四边形EBFD的周长为3x＋5x＋6x＋3x＋5x=22x， 　　由已知22x=66，得x=3． 　　所以ED=3x=3×3=9(cm)，AC=8x=8×3=24(cm)， 　　所以