题目内容
【题目】如图，直线y= 
与y轴交于点A，与直线y=﹣ 
交于点B，以AB为边向右作菱形ABCD，点C恰与原点O重合，抛物线y=（x﹣h）2+k的顶点在直线y=﹣ 上移动．若抛物线与菱形的边AB、BC都有公共点，则h的取值范围是（ ）
A.﹣2 
B.﹣2≤h≤1
C.﹣1 
D.﹣1
【答案】A
【解析】解：∵将y= 
与y=﹣ 
联立得： 
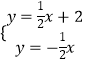，解得： 
．
∴点B的坐标为（﹣2，1）．
由抛物线的解析式可知抛物线的顶点坐标为（h，k）．
∵将x=h，y=k，代入得y=﹣ 得：﹣ 
h=k，解得k=﹣ 
，
∴抛物线的解析式为y=（x﹣h）2﹣ h．
如图1所示：当抛物线经过点C时．
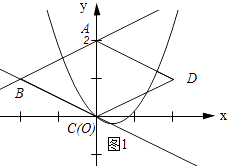
将C（0，0）代入y=（x﹣h）2﹣ h得：h2﹣ h=0，解得：h1=0（舍去），h2= ．
如图2所示：当抛物线经过点B时．
将B（﹣2，1）代入y=（x﹣h）2﹣ h得：（﹣2﹣h）2﹣ h=1，整理得：2h2+7h+6=0，解得：h1=﹣2，h2=﹣ 
（舍去）．
综上所述，h的范围是﹣2≤h≤ ．
所以答案是：A．
练习册系列答案
相关题目
