Question

将两个全等的直角三角形△ABC和△DEB按图1方式摆放，其中∠ACB=∠DEB=90゜，∠A=∠D=30゜，点E落在AB上．DE所在直线交AC所在直线于点F
（1）求证：AF+EF=DE；
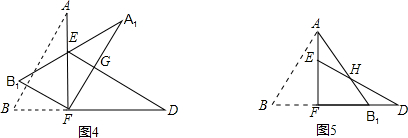
（2）若将图1中的△DBE绕点B按顺时针方向旋转α，且0゜＜α＜60゜，画出图形并证明AF+EF=DE；
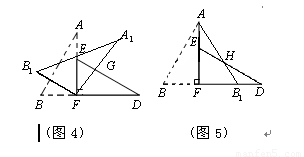
（3）若将图1中的△DBE绕点B按顺时针方向旋转角β，且60゜＜β＜180゜，求证：AF-EF=DE．

Answer 1

分析：（1）利用旋转的性质以及全等三角形的判定得出Rt△BCF≌Rt△BEF，进而得出答案；
（2）利用旋转的性质以及全等三角形的判定得出Rt△BCF≌Rt△BEF，进而得出答案；
（3）利用旋转的性质以及全等三角形的判定得出Rt△BCF≌Rt△BEF，进而得出答案．

解答：证明：（1）如图①所示，连接BF，
∵BC=BE，
在Rt△BCF和Rt△BEF中

BF=BF BC=BE

∴Rt△BCF≌Rt△BEF（HL），
∴EF=CF，
∴AF+EF=AC=DE；

（2）如图②所示：
延长DE交AC与点F，连接BF，
在Rt△BCF和Rt△BEF中

BF=BF BC=BE

∴Rt△BCF≌Rt△BEF（HL），
∴EF=CF，
∴AF+EF=AC=DE；

 （3）如图③所示：
连接BF，
在Rt△BCF和Rt△BEF中

BF=BF BC=BE

∴Rt△BCF≌Rt△BEF（HL），
∴EF=CF，
∴AF-FC=AC=DE，
∴AF-EF=DE．

点评：此题主要考查了全等三角形的判定与性质以及旋转的性质，根据已知得出全等三角形是解题关键．