题目内容
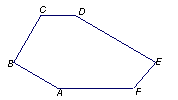
如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠BCD=124°,∠DEF=80°.
(1)观察直线AB与直线DE的位置关系,你能得出什么结论并说明理由;
(2)试求∠AFE的度数.
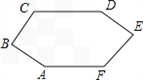
解:(1)AB∥DE.
理由如下:
延长AF、DE相交于点G,
∴CD∥AF,
∴∠CDE+∠G=180°.
∴∠CDE=∠BAF,
∴∠BAF+∠G=180°,
∴AB∥DE;
(2)延长BC、ED相交于点H.
∵AB⊥BC,
∴∠B=90°.
∵AB∥DE,
∴∠H+∠B=180°,
∴∠H=90°.
∵∠BCD=124°,
∴∠DCH=56°,
∴∠CDH=34°,
∴∠G=∠CDH=34°.
∵∠DEF=80°,
∴∠EFG=80°﹣34°=46°,
∴∠AFE=180°﹣∠EFG=180°﹣46°=134°.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
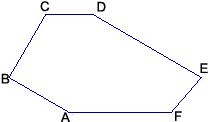 28、如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.
28、如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.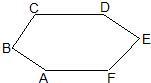 29、如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠BCD=124°,∠DEF=80°.
29、如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠BCD=124°,∠DEF=80°.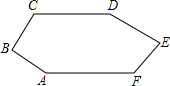 (2013•河西区一模)如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=124°,∠E=80°,则∠F=
(2013•河西区一模)如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=124°,∠E=80°,则∠F=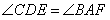 ,
,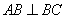 ,
,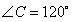 ,
,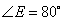 ,试求
,试求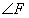 的度数.
的度数.