题目内容
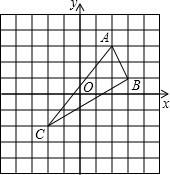
 如图,已知△ABC,O是△ABC内的一点,连接OB、OC,将∠ABO、∠ACO分别记为∠1、∠2,则∠1、∠2、∠A、∠O四个角之间的数量关系是( )
如图,已知△ABC,O是△ABC内的一点,连接OB、OC,将∠ABO、∠ACO分别记为∠1、∠2,则∠1、∠2、∠A、∠O四个角之间的数量关系是( )分析:连接AO并延长,交BC于点D,由三角形外角的性质可知∠BOD=∠BAD+∠1,∠COD=∠CAD+∠2,再把两式相加即可得出结论.
解答: 解:连接AO并延长,交BC于点D,
解:连接AO并延长,交BC于点D,
∵∠BOD是△AOB的外角,∠COD是△AOC的外角,
∴∠BOD=∠BAD+∠1①,∠COD=∠CAD+∠2②,
①+②得,∠BOC=(∠BAD+∠CAD)+∠1+∠2,即∠BOC=∠BAC+∠1+∠2.
故选D.
 解:连接AO并延长,交BC于点D,
解:连接AO并延长,交BC于点D,∵∠BOD是△AOB的外角,∠COD是△AOC的外角,
∴∠BOD=∠BAD+∠1①,∠COD=∠CAD+∠2②,
①+②得,∠BOC=(∠BAD+∠CAD)+∠1+∠2,即∠BOC=∠BAC+∠1+∠2.
故选D.
点评:本题考查的是三角形外角的性质,熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键.

练习册系列答案
相关题目
 24、如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH.
24、如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH. 如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.
如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°. 17、(1)已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h(要求尺规作图,不写作法和证明)
17、(1)已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h(要求尺规作图,不写作法和证明)
 20、如图,已知△ABC是锐角三角形,且∠A=50°,高BE、CF相交于点O,求∠BOC的度数.
20、如图,已知△ABC是锐角三角形,且∠A=50°,高BE、CF相交于点O,求∠BOC的度数.