题目内容
在战胜1998年的松花江特大洪水期间，为了加固一段松花江大堤，需运来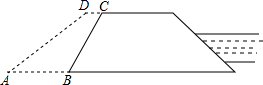
砂石和土将堤面加宽1米，使坡度由原来的1：2变成1：3，已知原来的背水坡长BC=5米，堤长100米．
①求水坝加宽部分的截面积SABCD；
②那么需要运来砂石和土多少立方米？（保留1位小数，参考数据：
=1.7，
=2.3，
=2.7）
砂石和土将堤面加宽1米，使坡度由原来的1：2变成1：3，已知原来的背水坡长BC=5米，堤长100米．①求水坝加宽部分的截面积SABCD；
②那么需要运来砂石和土多少立方米？（保留1位小数，参考数据：
| 3 |
| 5 |
| 7 |
分析：过点C作CE⊥AB，垂足为E，过D作DF⊥AB，垂足为F，设CE=x，则BE=2x，则DF=CE=x，AF=3x，在Rt△BCE中利用勾股定理可求出x的值，然后求出相关线段的长度，代入梯形的面积公式即可．
解答：解：①过C作CE⊥AB，垂足为E，
设CE=x，则BE=2x，则DF=CE=x，AF=3x，
AB=AF-BF=AF-（BE-EF）=3x-（2x-1）=x+1，
在Rt△CEB中，∠BEC=90°，BC=5，
则x2+（2x）2=52，
解得：x=
，
∴CE=
，AB=
+1，
∴S梯形ABCD=
（DC+AB）×DF=
×（
+2）×
=（
+
）≈4.8米2，
②需沙石和土：V=（
+
）×100=250+100
≈480（m3）．
设CE=x，则BE=2x，则DF=CE=x，AF=3x，
AB=AF-BF=AF-（BE-EF）=3x-（2x-1）=x+1，
在Rt△CEB中，∠BEC=90°，BC=5，
则x2+（2x）2=52，
解得：x=
| 5 |
∴CE=
| 5 |
| 5 |
∴S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
| 5 |
②需沙石和土：V=（
| 5 |
| 2 |
| 5 |
| 5 |
点评：本题考查了解直角三角形的运用，坡度坡角问题，关键过梯形上底的两个端点作梯形的高，将问题转化为解直角三角形的知识解题．
练习册系列答案
相关题目
在1998年的特大洪水期间，为了加固一段大堤，需运来沙石和土将大堤堤面加宽1米，使背水坡的坡度由原来的1：2变为1：3，已知原来背水坡的坡长为BC=15米，堤长100米，那么需要的沙石和土多少方？我国政府为保护农民利益，对某种农产品实行保护价格敞开收购，该农产品在1998年因市场因素降价30%后，到2002年保护价格为a，相比1998年的价格涨幅达60%，则该农产品在1998年降价前的价格为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
砂石和土将堤面加宽1米，使坡度由原来的1：2变成1：3，已知原来的背水坡长BC=5米，堤长100米．
，
，
）
，
，
）