题目内容
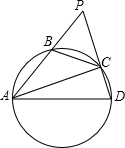 如图,已知ABCD是一个半径为R的圆内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于点P,且BP=8,∠APD=60°,则R=
如图,已知ABCD是一个半径为R的圆内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于点P,且BP=8,∠APD=60°,则R=分析:首先根据切割线定理即可计算出PC的长度是10,则PC=12AP,以及∠APD=60°,可以证明∠PCA=90°,在直角△ACD中根据勾股定理即可求得直径AD的长,从而求得半径的长.
解答:解:由切割线定理得PB•PA=PC•PD,则有
8×20=PC(PC+6).
解得PC=10.
在△PAC中,由PA=2PC,∠APC=60°,得∠PCA=90°.
从而AD是圆的直径.由勾股定理,得
AD2=AC2+CD2=(PA2-PC2)+CD2=202-102+62=336.
∴AD=
=4
∴R=
AD=2
.
故答案为2
.
8×20=PC(PC+6).
解得PC=10.
在△PAC中,由PA=2PC,∠APC=60°,得∠PCA=90°.
从而AD是圆的直径.由勾股定理,得
AD2=AC2+CD2=(PA2-PC2)+CD2=202-102+62=336.
∴AD=
| 336 |
| 21 |
∴R=
| 1 |
| 2 |
| 21 |
故答案为2
| 21 |
点评:本题主要考查了切割线定理,正确判定△ACD是直角三角形是解题的关键.

练习册系列答案
相关题目
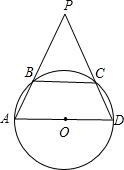 如图,已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为( )
如图,已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为( )| A、25π | B、16π | C、15π | D、13π |
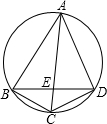 如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于
如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于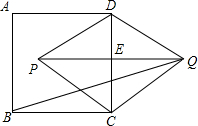 如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么tan∠PQB的值为
如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么tan∠PQB的值为 如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.
如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.