题目内容
(1998•苏州)已知点A(m,2)和点B(2,n)都在反比例函数y=
的图象上.
(1)求m与n的值;
(2)若直线y=mx-n与x轴交于点C,求点C关于y轴的对称点C′的坐标.
| m+3 | x |
(1)求m与n的值;
(2)若直线y=mx-n与x轴交于点C,求点C关于y轴的对称点C′的坐标.
分析:(1)把A的坐标代入y=
得出2=
,求出m,得出反比例函数的解析式y=
,把B的坐标代入求出n即可;
(2)把m=3,n=3代入直线y=mx-n得出y=3x-3,求出C的坐标,根据对称性质求出点C关于y轴的对称点C′的坐标即可.
| m+3 |
| x |
| m+3 |
| m |
| 6 |
| x |
(2)把m=3,n=3代入直线y=mx-n得出y=3x-3,求出C的坐标,根据对称性质求出点C关于y轴的对称点C′的坐标即可.
解答:解:(1)把A的坐标代入y=
得:2=
,
解得:m=3,
∴y=
,
把B的坐标代入y=
得:n=
=3,
即m=3,n=3.
(2)把m=3,n=3代入直线y=mx-n得:y=3x-3,
把y=0代入y=3x-3得:0=3x-3,
x=1,
即C的坐标是(1,0),
∴点C关于y轴的对称点C′的坐标是(-1,0).
| m+3 |
| x |
| m+3 |
| m |
解得:m=3,
∴y=
| 6 |
| x |
把B的坐标代入y=
| 6 |
| x |
| 6 |
| 2 |
即m=3,n=3.
(2)把m=3,n=3代入直线y=mx-n得:y=3x-3,
把y=0代入y=3x-3得:0=3x-3,
x=1,
即C的坐标是(1,0),
∴点C关于y轴的对称点C′的坐标是(-1,0).
点评:本题考查了用待定系数法求反比例函数的解析式,反比例函数和一次函数图象上点的坐标特征,轴对称的性质等知识点的应用,主要考查学生计算能力和理解能力.

练习册系列答案
相关题目
 (1998•苏州)已知四边形ABCD内接于圆,∠A=2∠C,则∠C等于( )
(1998•苏州)已知四边形ABCD内接于圆,∠A=2∠C,则∠C等于( )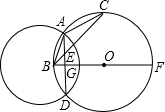 (1998•苏州)已知:如图,△ABC内接于⊙O,⊙B与⊙O相交于点A、D、AD交BC于点E,交⊙O的直径BF于点G.
(1998•苏州)已知:如图,△ABC内接于⊙O,⊙B与⊙O相交于点A、D、AD交BC于点E,交⊙O的直径BF于点G.