题目内容
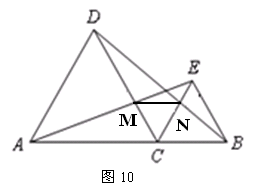
如图10,C是线段AB上的一点,△ACD和△BCE都是等边三角形.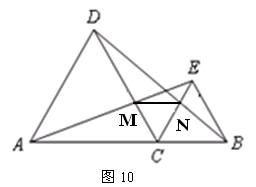
(1)求证:AE=BD;
(2)若AE交CD于M,BD交CE于N,连结MN,试判断△MCN的形状,并说明理由.
(1)证明略
(2)等边三角形,理由略解析:
(1)证明:∵△ACD和△BCE都是等边三角形
∴AC=CD,CE=CB,∠ACD=∠BCE=60°…………………………………1分
∵∠ACD+∠DCE=∠BCE+∠DCE
∴∠ACE=∠DCB………………………………………………………………2分
∴△ACE≌△DCB
∴AE=BD…………………………………………………………………………3分
(2)△MCN是等边三角形…………………………………………………………4分
∵∠ACD=∠BCE=60°,∠ACB是一个平角
∴∠DCE=60°
即∠ACM=∠DCN…………………………………………………………………5分
由(1)得△ACE≌△DCB
∴∠CAM=∠CDN…………………………………………………………………6分
又AC=DC
∴△ACM≌△DCN…………………………………………………………………7分


练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目

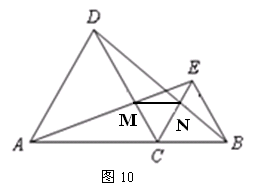
 和△BCE都是等边三角形.
和△BCE都是等边三角形.