题目内容
如图, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点![]() 从
从![]() 出发以每
出发以每
秒2个单位长度的速度向![]() 运动;点
运动;点![]() 从
从![]() 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向![]() 运动.其中一个
运动.其中一个
动点到达终点时,另一个动![]() 点也随之停止运动.过点
点也随之停止运动.过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,连结AC交NP于Q,连
,连结AC交NP于Q,连
结MQ. (1)点 (填M或N)能到达终点;(2)求△AQM的面积S与运动时间t的函数关系式,
并写出自变量t的取值范围,当t为何值时,S的值最大;
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的![]() 坐标,若不存在,说明理由.
坐标,若不存在,说明理由.
 | |||||||
解:(1)点 M
(2)经过t秒时,![]() ,
,![]() ,则
,则![]() ,
,![]()
∵![]() =
=![]() =
=![]() ,∴
,∴![]() ∴
∴![]()
∴![]()
![]()
∴![]()
∵![]() ∴当
∴当![]() 时,S的值最大.
时,S的值最大.
(3)存在。
设经过t秒时,NB=t,OM=2t ,则![]() ,
,![]() ,∴
,∴![]() =
=![]() =
=![]()
①若![]()
![]() ,则
,则![]() 是等腰Rt△
是等腰Rt△![]() 底边
底边![]() 上的高,∴
上的高,∴![]() 是底边
是底边![]() 的中线 ∴
的中线 ∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴点
,∴点![]() 的坐标为(1,0)
的坐标为(1,0)
②若![]() ,此时
,此时![]() 与
与![]() 重合,∴
重合,∴![]() ,∴
,∴![]() ,∴
,∴![]()
∴点![]() 的坐标为(2,0)
的坐标为(2,0)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
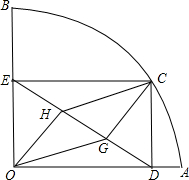 如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是
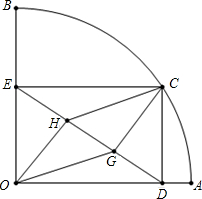 如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是 30、如图,四边形ABCD是一个正方形.
30、如图,四边形ABCD是一个正方形.
 如图,四边形OABC是矩形,点A、C的坐标分别为(3,0)、(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线
如图,四边形OABC是矩形,点A、C的坐标分别为(3,0)、(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线