题目内容
【题目】如图,圆心角∠AOB=120°,弦AB=2 ![]() cm.
cm.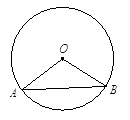
(1)求⊙O的半径r;
(2)求劣弧 ![]() 的长(结果保留
的长(结果保留 ![]() ).
).
【答案】
(1)解:作OC⊥AB于C,则AC= ![]() AB=
AB= ![]() cm.
cm.
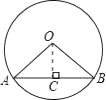
∵∠AOB=120°,OA=OB∴∠A=30°.
∴在Rt△AOC中,r=OA= ![]() =2cm
=2cm
(2)解:劣弧AB的长= ![]() πr=
πr= ![]() πcm
πcm
【解析】(1)根据垂径定理求出AC的值,由∠AOB的值,求出∠A的度数,根据三角函数求出⊙O的半径r;(2)根据弧长公式l=![]() πr,求出劣弧AB的长.
πr,求出劣弧AB的长.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对弧长计算公式的理解,了解若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.

练习册系列答案
相关题目