题目内容
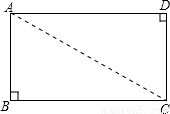
 如图,矩形纸片ABCD中,AD=3cm,点E在BC上,将纸片沿AE折叠,使点B落在AC上的点F处,且
如图,矩形纸片ABCD中,AD=3cm,点E在BC上,将纸片沿AE折叠,使点B落在AC上的点F处,且
∠AEF=∠CEF,则AB的长是
- A.1cm
- B.
 cm
cm - C.2cm
- D.
 cm
cm
B
分析:由矩形与折叠的性质,易求得∠AEB=60°,∠CAE=∠ACE=30°,根据等角对等边,可得AE=CE,由三角函数的性质,可得AE=2BE,可得BC=AD=3BE,即可求得BE的长,继而求得AB的长.
解答:∵四边形ABCD是矩形,
∴∠B=90°,BC=AD=3cm,
由折叠的性质可得:∠AEB=∠AEF,∠BAE=∠CAE,
∵∠AEF=∠CEF,
∴∠AEB=∠AEF=∠CEF= ×180°=60°,
×180°=60°,
∴∠BAE=90°-∠AEB=30°,
∴AB=BE•tan∠AEB= BE,AE=2BE,∠CAE=∠BAE=30°,
BE,AE=2BE,∠CAE=∠BAE=30°,
∴∠BAC=60°,
∴∠ACB=90°-∠BAC=30°,
∴∠CAE=∠ACE,
∴AE=CE,
∴CE=2BE,
∴BE=BE+CE=3BE=3cm,
∴BE=1cm,
∴AB= BE=
BE= (cm).
(cm).
故选B.
点评:此题考查了折叠的性质、矩形的性质、等腰三角形的判定与性质以及三角函数的知识.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.
分析:由矩形与折叠的性质,易求得∠AEB=60°,∠CAE=∠ACE=30°,根据等角对等边,可得AE=CE,由三角函数的性质,可得AE=2BE,可得BC=AD=3BE,即可求得BE的长,继而求得AB的长.
解答:∵四边形ABCD是矩形,
∴∠B=90°,BC=AD=3cm,
由折叠的性质可得:∠AEB=∠AEF,∠BAE=∠CAE,
∵∠AEF=∠CEF,
∴∠AEB=∠AEF=∠CEF=
 ×180°=60°,
×180°=60°,∴∠BAE=90°-∠AEB=30°,
∴AB=BE•tan∠AEB=
 BE,AE=2BE,∠CAE=∠BAE=30°,
BE,AE=2BE,∠CAE=∠BAE=30°,∴∠BAC=60°,
∴∠ACB=90°-∠BAC=30°,
∴∠CAE=∠ACE,
∴AE=CE,
∴CE=2BE,
∴BE=BE+CE=3BE=3cm,
∴BE=1cm,
∴AB=
 BE=
BE= (cm).
(cm).故选B.
点评:此题考查了折叠的性质、矩形的性质、等腰三角形的判定与性质以及三角函数的知识.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
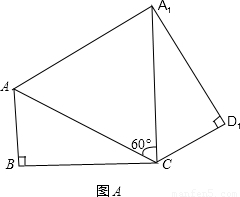
 如图,矩形纸片ABCD中,AB=4,BC=4
如图,矩形纸片ABCD中,AB=4,BC=4

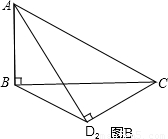
 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E. ,将矩形沿对角线AC剪开,解答以下问题:
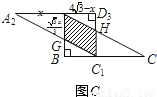
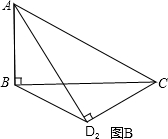
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



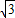 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: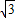 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.