题目内容
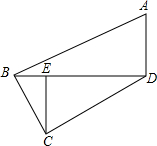
已知，四边形ABCD中，∠ABC=∠ADB=90°，CE⊥BD于E，AB=5，AD=3，BC=2
，求四边形ABCD的面积S四边形ABCD．
| 3 |
在Rt△ABD中，AB=5，AD=3，
∴BD=
=
=4，
∵∠ABD+∠CBD=∠BCE+∠CBD=90°，
∴∠ABD=∠BCE，
∴cos∠ABD=
=
=cos∠BCE=
=
，
解得：CE=
，
∴S四边形ABCD=S△ABD+S△BCD=
AD×BD+
BD×CE=
×3×4+
×4×
=6+
．
∴BD=
| AB2-AD2 |
| 52-32 |
∵∠ABD+∠CBD=∠BCE+∠CBD=90°，
∴∠ABD=∠BCE，
∴cos∠ABD=
| BD |
| AB |
| 4 |
| 5 |
| CE |
| BC |
| CE | ||
2
|
解得：CE=
8
| ||
| 5 |
∴S四边形ABCD=S△ABD+S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
8
| ||
| 5 |
16
| ||
| 5 |
练习册系列答案
小题狂做系列答案
相关题目
