题目内容
已知：如图，AD⊥BC，垂足为D，且AB2=BD•BC
求证：△ABC是直角三角形．
证明：∵AB2=BD•BC
∴
=
∵∠B=∠B
∴△ABC∽△DBA
∵AD⊥BC
∴∠BAC=∠BDA=90°
∴△ABC是直角三角形．
分析：由于AB2=BD•BC，∠B=∠B，可知△ABC∽△DBA，由AD⊥BC可知∠BAC=∠BDA=90°，故△ABC是直角三角形．
点评：本题考查的是相似三角形的判定定理，及垂直的性质．
∴
=∵∠B=∠B
∴△ABC∽△DBA
∵AD⊥BC
∴∠BAC=∠BDA=90°
∴△ABC是直角三角形．
分析：由于AB2=BD•BC，∠B=∠B，可知△ABC∽△DBA，由AD⊥BC可知∠BAC=∠BDA=90°，故△ABC是直角三角形．
点评：本题考查的是相似三角形的判定定理，及垂直的性质．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
27、已知：如图，AD∥BC，ED∥BF，且AF=CE．
25、已知，如图，AD∥BC，∠1=∠2，∠A=120°，且BD⊥CD，求∠C的度数．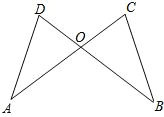
已知：如图，AD=BC，AC=BD．试判断OD、OC的数量关系，并说明理由．
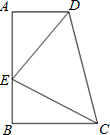已知，如图，AD∥BC，∠A=90°，AD=BE，∠EDC=∠ECD，请你说明下列结论成立的理由：（1）△AED≌△BCE，（2）AB=AD+BC．
根据题意填空：