题目内容
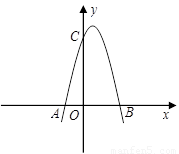
已知抛物线 与
与 轴交于两点A
轴交于两点A ,B
,B ,且
,且 ,求k的值.
,求k的值.
【答案】

【解析】
试题分析:由抛物线与 轴交于两点,可得△﹥0,由题意知方程
轴交于两点,可得△﹥0,由题意知方程 的两根为
的两根为 .
.
由韦达定理得:

 解得:
解得: ;把k的值代入△﹥0验证,当
;把k的值代入△﹥0验证,当 时,满足;当
时,满足;当 时,不满足;所以
时,不满足;所以 .
.
试题解析: 抛物线与
抛物线与 轴交于两点,
轴交于两点,
 ①
①
由题意知方程 的两根为
的两根为 .
.
由韦达定理得:


即: ,解得:
,解得: ;
;
当 时,代入①满足;当
时,代入①满足;当 时,代入①不满足;
时,代入①不满足;
综上, .
.
考点:1.韦达定理.2.根的判别式.3. 抛物线与一元二次方程的关系.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
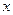 轴交于A(1,0),B(
轴交于A(1,0),B(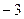 ,0)两点,与
,0)两点,与 轴交于点
轴交于点
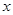 轴交于A (-4,0) 和B(1,0)两点,与
轴交于A (-4,0) 和B(1,0)两点,与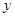 轴交于C(0,-2)点.
轴交于C(0,-2)点.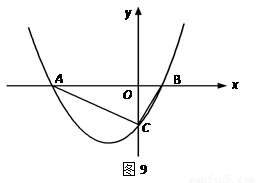
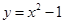 与
与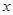 轴交于A、B两点,与
轴交于A、B两点,与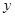 轴交于点C.
轴交于点C.
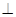
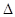 PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
PCA相似.若存在,请求出M点的坐标;否则,请说明理由.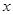 轴交于点
轴交于点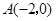 ,
,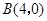 ,与
,与 轴交于点
轴交于点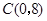 .
.
 的坐标;
的坐标;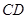 交
交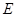 .在线段
.在线段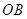 的垂直平分线上是否存在点
的垂直平分线上是否存在点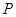 ,使得点
,使得点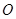 的距离?如果存在,求出点
的距离?如果存在,求出点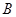 作
作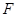 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段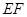 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?