Question

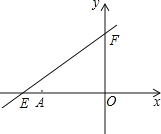
【题目】如图，直线y＝kx+6与x轴、y轴分别交于点E，F，点E的坐标为（﹣8，0），点A的坐标为（﹣6，0）

（1）求k的值；

（2）若点P（x，y）是第二象限内的直线上的一个动点，在点P的运动过程中，试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；

（3）在（2）的条件下，探究：当点P运动到什么位置时，△OPA的面积为，并说明理由；

（4）问在x轴上是否存在点Q，使得△EFQ为等腰三角形？若存在，求出符合条件的Q的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）k＝；（2）S＝x+18（﹣8＜x＜0）；（3）点P（﹣，）时，△OPA的面积为；（4）存在，符合条件的Q的坐标为（﹣18，0）或（2，0）或（8，0）或（﹣，0）

【解析】

（1）将点E的坐标代入解析式中即可求出结论；

（2）由题意可得y＝x+6，然后求出点A的坐标，根据三角形的面积公式即可求出结论；

（3）把S＝代入S＝x+18即可求出结论；

（4）根据等腰三角形腰的情况分类讨论，画出对应的图形，然后根据等腰三角形的性质和勾股定理即可求出结论．

解：（1）∵直线y＝kx+6经过点E（﹣8，0），

∴﹣8k+6＝0，

解得k＝；

（2）∵点P（x，y）是第二象限内的直线上的一个动点，

∴y＝x+6，

∵点A的坐标为（﹣6，0），

∴OA＝6，

∴S＝OAy＝×6×（x+6）＝x+18．

即S＝x+18（﹣8＜x＜0）；

（3）把S＝代入S＝x+18

得＝x+18，

解得x＝﹣，

∴当点P（﹣，）时，△OPA的面积为；

（4）如图，∵E（﹣8，0），F（0，6）

∴OE＝8，OF＝6，EF＝10，

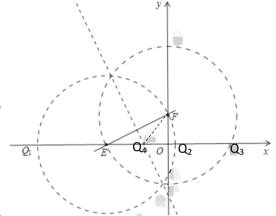
①以E为圆心以EF为半径作圆交x轴于Q1、Q2，

则Q1（﹣18，0），Q2（2，0），

②以F为圆心以EF为半径作圆交x轴于Q3，

易知FO垂直平分EQ3，

则Q3（8，0），

③作EF的垂直平分线交x轴于Q4，

∴Q4E= Q4F，设Q4O=x，则Q4E= Q4F=8－x，

由勾股定理可得

即

解得：x=

∴Q4（﹣，0）．

综上，符合条件的Q的坐标为（﹣18，0）或（2，0）或（8，0）或（﹣，0）．