题目内容
 (2013•绥化)如图,在Rt△ABC中,∠C=90°,AC=
(2013•绥化)如图,在Rt△ABC中,∠C=90°,AC=| 3 |
分析:先根据勾股定理计算出AB=2,根据含30度的直角三角形三边的关系得到∠BAC=30°,在根据折叠的性质得BE=BA=2,∠BED=∠BAD=30°,DA=DE,由于AD⊥ED得BC∥DE,所以∠CBF=∠BED=30°,在Rt△BCF中可计算出CF=
,BF=2CF=
,则EF=2-
,在Rt△DEF中计算出FD=1-
,ED=
-1,然后利用S△ABE=S△ABD+S△BED+S△ADE=2S△ABD+S△ADE计算即可.
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
| 3 |
解答:解:∵∠C=90°,AC=
,BC=1,
∴AB=
=2,
∴∠BAC=30°,
∵△ADB沿直线BD翻折后,点A落在点E处,
∴BE=BA=2,∠BED=∠BAD=30°,DA=DE,
∵AD⊥ED,
∴BC∥DE,
∴∠CBF=∠BED=30°,
在Rt△BCF中,CF=
=
,BF=2CF=
,
∴EF=2-
,
在Rt△DEF中,FD=
EF=1-
,ED=
FD=
-1,
∴S△ABE=S△ABD+S△BED+S△ADE
=2S△ABD+S△ADE
=2×
BC•AD+
AD•ED
=2×
×1×(
-1)+
×(
-1)(
-1)
=1.
故选A.
| 3 |
∴AB=
| AC2+BC2 |
∴∠BAC=30°,
∵△ADB沿直线BD翻折后,点A落在点E处,
∴BE=BA=2,∠BED=∠BAD=30°,DA=DE,
∵AD⊥ED,
∴BC∥DE,
∴∠CBF=∠BED=30°,
在Rt△BCF中,CF=
| BC | ||
|
| ||
| 3 |
2
| ||
| 3 |
∴EF=2-
2
| ||
| 3 |
在Rt△DEF中,FD=
| 1 |
| 2 |
| ||
| 3 |
| 3 |
| 3 |
∴S△ABE=S△ABD+S△BED+S△ADE
=2S△ABD+S△ADE
=2×
| 1 |
| 2 |
| 1 |
| 2 |
=2×
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
=1.
故选A.
点评:本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了勾股定理和含30度的直角三角形三边的关系.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 (2013•绥化)如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件
(2013•绥化)如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件 (2013•绥化)如图所示,以O为端点画六条射线后OA,OB,OC,OD,OE,O后F,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2013个点在射线
(2013•绥化)如图所示,以O为端点画六条射线后OA,OB,OC,OD,OE,O后F,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2013个点在射线 (2013•绥化)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是边AD,AB的中点,EF交AC于点H,则
(2013•绥化)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是边AD,AB的中点,EF交AC于点H,则 (2013•绥化)如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为( )
(2013•绥化)如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为( )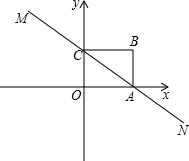 (2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.
(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.